题目内容

已知动圆M与圆F：x2+（y-2）2=1外切，与圆N：x2+y2+4y-77=0内切，求动圆圆心M所在的曲线C的方程．
分析：求出圆M和圆N的圆心和半径，由题意列出关于动圆圆心所满足的关系，整理后即可得到答案．
解答：解：∵圆F：x2+（y-2）2=1的圆心为（0，2），半径为1，
圆N：x2+y2+4y-77=0内的圆心为（0，-2），半径为9．
又动圆M与圆F：x2+（y-2）2=1外切，与圆N：x2+y2+4y-77=0内切，
设动圆圆心为（x，y）．
∴
x2+(y-2)2
-1=9-
x2+(y+2)2

整理得25x2+21y2=525
∴动圆圆心M所在的曲线C的方程为25x2+21y2=525．
点评：本题考查了椭圆的定义，考查了曲线方程的求法，关键是由题意列出动圆圆心所满足的关系式，是基础题．
练习册系列答案
相关题目
已知动圆M过定点F（0，-
2
），且与直线y=
2
相切，椭圆N的对称轴为坐标轴，一个焦点为F，点A（1，
2
）在椭圆N上．
（1）求动圆圆心M的轨迹Γ的方程及椭圆N的方程；
（2）若动直线l与轨迹Γ在x=-4处的切线平行，且直线l与椭圆N交于B，C两点，试求当△ABC面积取到最大值时直线l的方程．
已知动圆P与圆M：(x+
2
6
3
)2+y2=16相切，且经过点N(
2
6
3
，0)．
（1）试求动圆的圆心P的轨迹C的方程；
（2）设O为坐标原点，圆D：（x-t）2+y2=t2（t＞0），若圆D与曲线C交于关于x轴对称的两点A、B（点A的纵坐标大于0），且
OA
•
OB
=0，请求出实数t的值；
（3）在（2）的条件下，点D是圆D的圆心，E、F是圆D上的两动点，满足2
OD
=
OE
+
OF
，点T是曲线C上的动点，试求
TE
•
TF
的最小值．
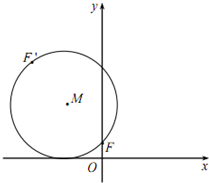（2012•深圳二模）如图，已知动圆M过定点F（0，1）且与x轴相切，点F关于圆心M的对称点为F′，动点F′的轨迹为C．
（1）求曲线C的方程；
（2）设A（x0，y0）是曲线C上的一个定点，过点A任意作两条倾斜角互补的直线，分别与曲线C相交于另外两点P、Q．
①证明：直线PQ的斜率为定值；
②记曲线C位于P、Q两点之间的那一段为l．若点B在l上，且点B到直线PQ的距离最大，求点B的坐标．

已知动圆M过定点F(2，0)，且与直线x＝－2相切，动圆圆心M的轨迹为曲线C

(1)求曲线C的方程

(2)若过F(2，0)且斜率为1的直线与曲线C相交于A，B两点，求|AB|

已知动圆M过定点F(2，0)，且与直线x＝－2相切，动圆圆心M的轨迹为曲线C

(1)求曲线C的方程

(2)若过F(2，0)且斜率为1的直线与曲线C相交于A，B两点，求|AB|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网