题目内容
(本小题满分14分)
已知函数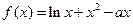 .
.
(Ⅰ)若函数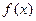 在其定义域上为增函数,求
在其定义域上为增函数,求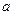 的取值范围;
的取值范围;
(Ⅱ)设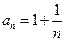 (
(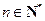 ),求证:
),求证:
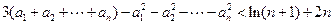 .
.
已知函数
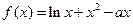 .
.(Ⅰ)若函数
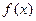 在其定义域上为增函数,求
在其定义域上为增函数,求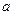 的取值范围;
的取值范围;(Ⅱ)设
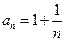 (
(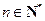 ),求证:
),求证: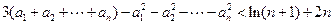 .
.(1)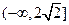 (2)略
(2)略
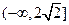 (2)略
(2)略(Ⅰ)函数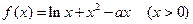 ,
,
则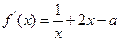
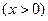 .………………………………………………3分
.………………………………………………3分
因为函数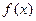 在
在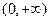 上是单调增函数,
上是单调增函数,
所以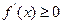 在
在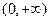 上恒成立.
上恒成立.
即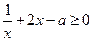 在
在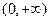 上恒成立.
上恒成立.
所以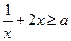 .
.
因为当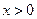 时,
时,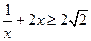 ,
,
当且仅当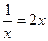 ,即
,即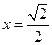 时等号成立.
时等号成立.
所以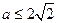 时.
时.
故实数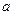 的取值范围是
的取值范围是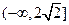 .…………………………………………………7分
.…………………………………………………7分
(Ⅱ)令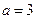 ,则
,则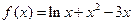 .
.
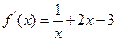
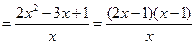 .
.
当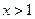 时,
时,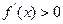 ,
,
所以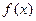 在
在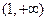 上是增函数.
上是增函数.
所以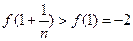 .
.
所以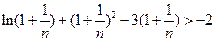 .
.
所以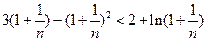 .
.
即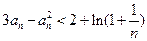 .…………………………………………………10分
.…………………………………………………10分
所以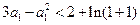 ,
,
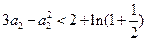 ,
,
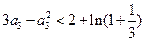 ,
,
……
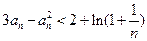 .
.
所以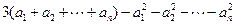
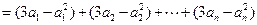
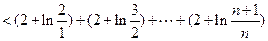
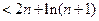 .
.
故所证不等式成立.……………………………………………………………14分
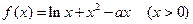 ,
,则
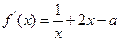
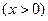 .………………………………………………3分
.………………………………………………3分因为函数
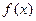 在
在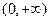 上是单调增函数,
上是单调增函数,所以
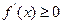 在
在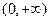 上恒成立.
上恒成立.即
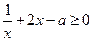 在
在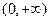 上恒成立.
上恒成立.所以
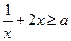 .
.因为当
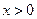 时,
时,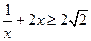 ,
,当且仅当
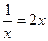 ,即
,即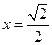 时等号成立.
时等号成立.所以
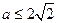 时.
时.故实数
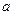 的取值范围是
的取值范围是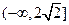 .…………………………………………………7分
.…………………………………………………7分(Ⅱ)令
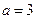 ,则
,则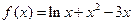 .
.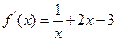
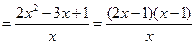 .
.当
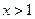 时,
时,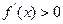 ,
,所以
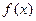 在
在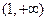 上是增函数.
上是增函数.所以
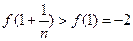 .
.所以
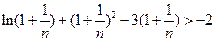 .
.所以
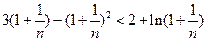 .
.即
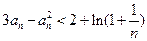 .…………………………………………………10分
.…………………………………………………10分所以
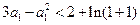 ,
,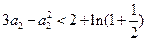 ,
,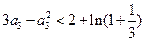 ,
,……
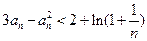 .
.所以
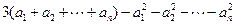
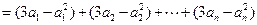
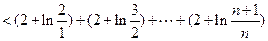
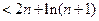 .
.故所证不等式成立.……………………………………………………………14分

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
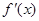 >0恒成立,则下列不等式成立的是
>0恒成立,则下列不等式成立的是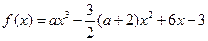 。
。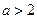 时,求函数
时,求函数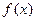 的极小值;
的极小值;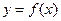 零点的个数。
零点的个数。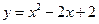 与
与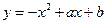
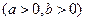 在它们的一个交点处切线互相垂直,则
在它们的一个交点处切线互相垂直,则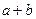 的值为
的值为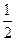
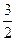
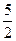

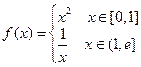 (其中
(其中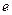 为自然对数的底数),则
为自然对数的底数),则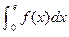 的值为
的值为 



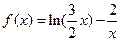 的零点一定位于( )
的零点一定位于( )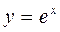 在点P处的切线斜率为e,则点P的坐标为( )
在点P处的切线斜率为e,则点P的坐标为( ) 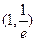
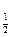 (2x2-3x+1)的递减区间为 ( )
(2x2-3x+1)的递减区间为 ( )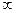 )
)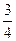 ]
]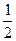 ,+
,+