题目内容
已知各项均为正数的等差数列{an}中，a2•a12=49，则a7的最小值为（ ）A．7
B．8
C．9
D．10
【答案】分析：由条件可得得 a7=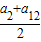
，再利用基本不等式a7的最小值．
解答：解：由等差数列的性质可得 a7=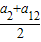
，
∵等差数列{an}中，各项均为正数，a2•a12=49，
∴
≥
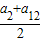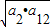=7，当且仅当 a2 =a12 时，等号成立，
故则a7的最小值为 7，
故选A．
点评：本题主要考查等差数列的性质应用，基本不等式的应用，属于中档题．
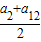，再利用基本不等式a7的最小值．解答：解：由等差数列的性质可得 a7=
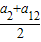，∵等差数列{an}中，各项均为正数，a2•a12=49，
∴
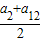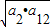≥=7，当且仅当 a2 =a12 时，等号成立，故则a7的最小值为 7，
故选A．
点评：本题主要考查等差数列的性质应用，基本不等式的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
中，
与
的等比中项为
，则
的最小值为（ ）
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
，
的等比中项。
是等差数列；
的前n项和为Tn,求Tn。
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。