题目内容
设圆锥曲线C1的焦点为F(0,(1)求C1的方程;
(2)设曲线C2:x2+y2=5,过点P(0,a)作与y轴不垂直的直线m交C1于A,D两点,交C2于B,C两点,且![]() =
=![]() ,求实数a的取值范围.
,求实数a的取值范围.
解:(1)∵e= =1,
=1,

∴C1为抛物线,其中顶点为(0,-7),开口向上,p=![]() ,方程为y=x2-7.①
,方程为y=x2-7.①
(2)![]() =CD.∴|AB|=|CD|,无论A、B、C、D的顺序如何,均有AD的中点与BC的中点重合.直线m与两轴都不垂直,设AD:y=kx+a,②
=CD.∴|AB|=|CD|,无论A、B、C、D的顺序如何,均有AD的中点与BC的中点重合.直线m与两轴都不垂直,设AD:y=kx+a,②
联立①②,得x2-7=kx+a,即x2-kx-(a+7)=0.
设A(x1,y1),D(x2,y2),M(x0,y0),则x1+x2=k,x0=![]() ,代入②,得y0=
,代入②,得y0=![]() +a.
+a.
∴M(![]() ,
,![]() +a).14分∵AD的中点与BC的中点重合,而BC⊥OM,
+a).14分∵AD的中点与BC的中点重合,而BC⊥OM,
∴AD⊥OM.∴ ·k=-1,③即k2=-2a-1.
·k=-1,③即k2=-2a-1.
当且仅当点M在圆内部时,直线m与圆相交且与抛物线也相交,∴(![]() )2+(
)2+(![]() +a)2<5.④
+a)2<5.④
由③,得-2a-1>0,∴a<![]() .③代入④,得a>-10.∴a的取值范围是-10<a<
.③代入④,得a>-10.∴a的取值范围是-10<a<![]() .
.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: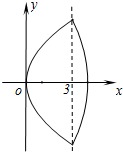 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: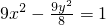 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;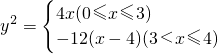 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 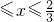 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: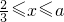 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.