题目内容
函数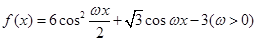 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形
为正三角形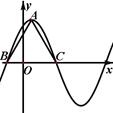
(1)求 的值及函数
的值及函数 的值域;
的值域;
(2)若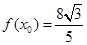 ,且
,且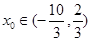 ,求
,求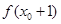 的值.
的值.
(1) ,
, ;(2)
;(2)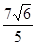
解析试题分析:(1)利用两角和正弦公式和降幂公式化简,得到 的形式,利用公式
的形式,利用公式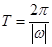 计算周期,求三角函数的最小正周期一般化成先化简成
计算周期,求三角函数的最小正周期一般化成先化简成 ,
,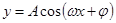 ,
,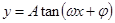 形式,利用周期公式即可;(2)利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角
形式,利用周期公式即可;(2)利用平方关系解决问题时,要注意开方运算结果的符号,需要根据角 的范围确定,二是利用诱导公式进行化简时,(3)三角函数的给值求值的问题一般是正用公式将“复角”展开,看需要求相关角的哪些三角函数值,然后根据角的范围求出相应角三角函数值,代入展开即可,注意角的范围.
的范围确定,二是利用诱导公式进行化简时,(3)三角函数的给值求值的问题一般是正用公式将“复角”展开,看需要求相关角的哪些三角函数值,然后根据角的范围求出相应角三角函数值,代入展开即可,注意角的范围.
试题解析:解:(1)由已知可得: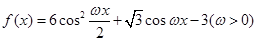
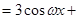

又由于正三角形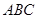 的高为2
的高为2 ,则
,则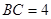
所以,函数
所以,函数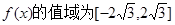
(2)因为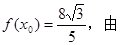 (1)有
(1)有
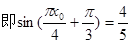
由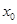

所以,
故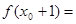
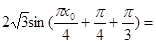

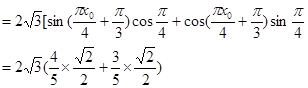
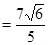 .
.
考点:1、求三角函数的值域;2、三角函数给值求值的问题.

练习册系列答案
相关题目
在区间 上随机取一个
上随机取一个 ,
, 的值介于
的值介于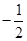 与
与 之间的概率为( )
之间的概率为( )
A. | B. | C. | D. |
复数 ,则
,则 的共轭复数
的共轭复数 在复平面内对应的点( ).
在复平面内对应的点( ).
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知圆 与圆
与圆 相外切, 则
相外切, 则 的最大值为 ( )
的最大值为 ( )
A. | B. | C. | D. |
 ,
, ,那么
,那么 是
是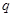 的 .(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要”中选择一个填空)
的 .(在“充分不必要条件”、“必要不充分条件”、“充要条件”、“既不充分也不必要”中选择一个填空) ,其中
,其中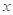 是仪器的月产量,
是仪器的月产量,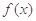 表示为月产量
表示为月产量 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 .
. 的值;
的值; ,求
,求 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= . 的前n项和
的前n项和 ,则
,则 = .
= .