题目内容
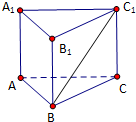 如图,正三棱柱A1B1C1-ABC中,AB=2,AA1=
如图,正三棱柱A1B1C1-ABC中,AB=2,AA1=| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
分析:取A1B1的中点D,连接BD,则C1D⊥面ABB1A1,可得∠C1DB为BC1与面ABB1A1所成的角,证明C1D=BD,可得结论.
解答: 解:取A1B1的中点D,连接BD,则C1D⊥面ABB1A1,
解:取A1B1的中点D,连接BD,则C1D⊥面ABB1A1,
∴∠C1DB为BC1与面ABB1A1所成的角.
∵正三棱柱A1B1C1-ABC中,AB=2,AA1=
,
∴C1D=BD=
,
∴∠C1DB=45°,即BC1与面ABB1A1所成的角大小是45°.
故选:B.
 解:取A1B1的中点D,连接BD,则C1D⊥面ABB1A1,
解:取A1B1的中点D,连接BD,则C1D⊥面ABB1A1,∴∠C1DB为BC1与面ABB1A1所成的角.
∵正三棱柱A1B1C1-ABC中,AB=2,AA1=
| 2 |
∴C1D=BD=
| 3 |
∴∠C1DB=45°,即BC1与面ABB1A1所成的角大小是45°.
故选:B.
点评:本题考查线面角,考查学生的计算能力,正确作出线面角是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
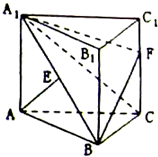 如图,正三棱柱ABC-A1B1C1中,侧面AA1C1C是边长为2的正方形,E是A1B的中点,F在棱CC1上.
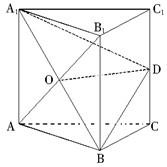
如图,正三棱柱ABC-A1B1C1中,侧面AA1C1C是边长为2的正方形,E是A1B的中点,F在棱CC1上.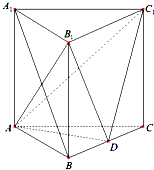 如图,正三棱柱ABC-A1B1C1的侧棱长和底面长均为2,D为BC中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面长均为2,D为BC中点. (2003•北京)如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AB=a.
(2003•北京)如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AB=a.