Question

18．当k为什么实数时，方程组$\left\{\begin{array}{l}{4x+3y=60}\\{kx+（k+2）y=60}\end{array}\right.$的解满足x＞y＞0的条件？

Answer 1

分析 由题意知直线kx+（k+2）y=60恒过点A（-30，30）；从而作出直线，由数形结合求解即可．

解答 解：由题意作图象如下，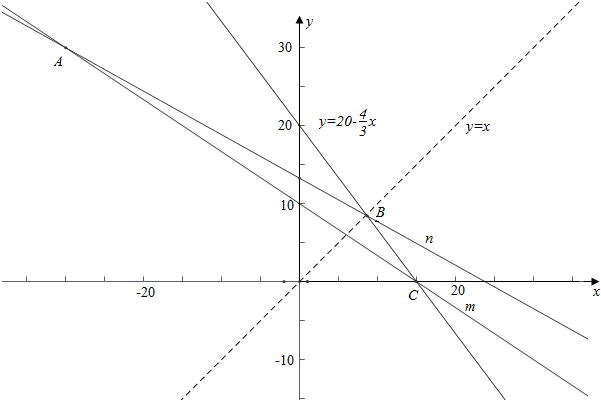

易知直线kx+（k+2）y=60恒过点A（-30，30）；
当直线kx+（k+2）y=60过点C（15，0）时，k_m=$\frac{0-30}{15+30}$=-$\frac{2}{3}$，
当直线kx+（k+2）y=60过点B（$\frac{60}{7}$，$\frac{60}{7}$）时，k_m=$\frac{\frac{60}{7}-30}{\frac{60}{7}+30}$=-$\frac{5}{9}$，
故结合图象可知，直线kx+（k+2）y=60的斜率$-\frac{k}{k+2}$满足，
-$\frac{2}{3}$＜$-\frac{k}{k+2}$＜-$\frac{5}{9}$，
解得，2.5＜k＜4．

点评 本题考查了直线与直线的交点的判断及数形结合的思想应用．