题目内容
定义:对于函数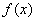 ,若在定义域内存在实数
,若在定义域内存在实数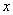 ,满足
,满足 ,则称
,则称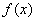 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数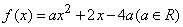 ,试判断
,试判断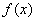 是否为定义域R上的“局部奇函数”?若是,求出满足
是否为定义域R上的“局部奇函数”?若是,求出满足 的x的值;若不是,请说明理由;
的x的值;若不是,请说明理由;
(2)若 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数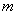 的取值范围;
的取值范围;
(3)若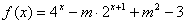 为定义域
为定义域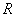 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数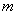 的取值范围.
的取值范围.
 (2)当
(2)当 时,
时,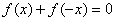 可化为
可化为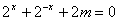
因为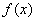 的定义域为
的定义域为 ,所以方程
,所以方程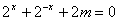 在
在 上有解.
上有解.
令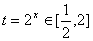 ,则
,则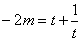 ;设
;设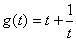 ,则
,则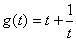 在
在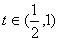 上为减函数,在
上为减函数,在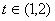 上为增函数,所以此时
上为增函数,所以此时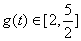 ,
,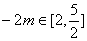 ,即
,即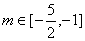 ……………8分
……………8分
(3)当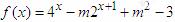 时,
时,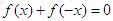 可化为
可化为
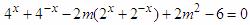
设 ,则
,则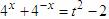
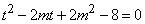 在
在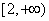 有解即可保证
有解即可保证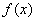 为“局部奇函数”.
为“局部奇函数”.
令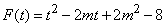 ,
,
1° 当 ,
,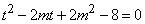 在
在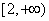 有解,
有解,
由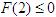 ,即
,即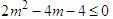 ,解得
,解得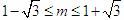
2° 当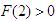 ,即
,即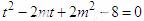 在
在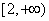 有解等价于
有解等价于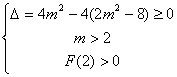 ,解得
,解得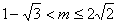
综上,所求实数m的取值范围为

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
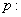 方程
方程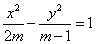 表示焦点在
表示焦点在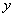 轴上的椭圆;命题
轴上的椭圆;命题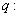 双曲线
双曲线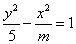 的离心率
的离心率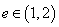 ,若
,若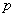 、
、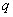 有且只有一个为真命题,求实数
有且只有一个为真命题,求实数 的取值范围.
的取值范围. 在某一个周期的图象时,列表并填入的部分数据如下表:
在某一个周期的图象时,列表并填入的部分数据如下表: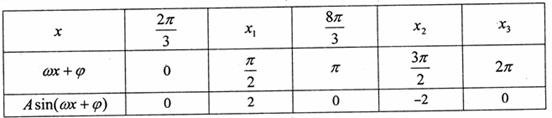
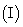 求
求 ,
,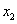 ,
, 的值及函数
的值及函数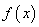 的表达式;
的表达式;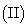 将函数
将函数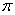 个单位,可得到函数
个单位,可得到函数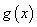 的图象,求函数
的图象,求函数 在区间
在区间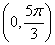 的最小值.
的最小值.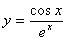 的图像大致是( )[来
的图像大致是( )[来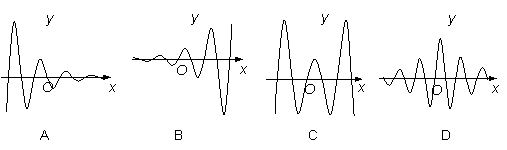
 ,
,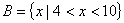 ,
,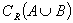 及
及 .
.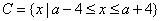 ,且
,且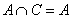 ,求
,求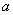 的取值范围.
的取值范围.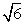 ,侧视图面积为
,侧视图面积为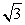 ,俯视图面积为
,俯视图面积为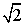 ,则长方体的外接球的
,则长方体的外接球的 B.
B.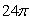 C.
C.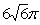 D.
D.
 是定义在
是定义在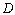 上的函数, 若存在区间
上的函数, 若存在区间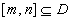 , 使函数
, 使函数 上的值域恰为
上的值域恰为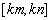 ,则称函数
,则称函数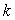 型函数.给出下列说法:①
型函数.给出下列说法:①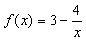 不可能是
不可能是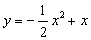 是
是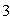 型函数, 则
型函数, 则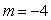 ,
,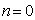 ;
;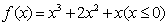 是
是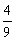 ;
; 是
是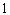 型函数, 则
型函数, 则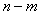 的最大值为
的最大值为 .
.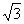 cosx,2cosx). 设函数f(x)=a
cosx,2cosx). 设函数f(x)=a b-
b-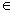 R)
R)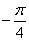 ,
,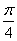 ]时,求f(x)的值域。
]时,求f(x)的值域。