Question

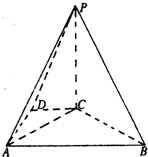在四棱锥P-ABCD中，PC⊥面ABCD，DC∥AB，DC=1，AB=4，BC=2

3

，∠CBA=30°．
（I）求证：AC⊥PB；
（II）当PD=2时，求此四棱锥的体积．

Answer 1

分析：（I）先在△ABC中，利用余弦定理，得出AC²+BC²=AB²，从而得出AC⊥BC，再结合PC⊥AC，而BC、PC是平面PBC内的相交直线，得到AC⊥平面PBC，最后根据线面垂直的定义，可证出AC⊥PB；
（II）过点C作CE⊥AB于E，在Rt△BCE中，利用三角函数的定义，得到CE=

1

2

BC=

3

，从而可得梯形ABCD的面积为

5 3

2

．再结合PC⊥平面ABCD，在Rt△PCD中，利用勾股定理算出PC=

3

，最后利用锥体的体积公式，得V_P-ABCD=

1

3

S_ABCD•PC=

1

3

•

5 3

2

•

3

=

5

2

．

解答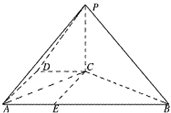：解：（I）∵△ABC中，AB=4，BC=2

3

，∠CBA=30°，
∴根据余弦定理，得AC²=AB²+BC²-2AB×BCcos∠CBA=4
∴AC²+BC²=4+12=16=AB²
∴AC⊥BC
又∵PC⊥平面ABCD，AC?平面ABCD
∴PC⊥AC
∵BC、PC是平面PBC内的相交直线
∴AC⊥平面PBC
∴结合BC?平面PBC，可得AC⊥BC
（II）过点C作CE⊥AB于E，
∵Rt△BCE中，BC=2

3

，∠ECB=30°
∴CE=

1

2

BC=

3

可得梯形ABCD的面积为：S_ABCD=

1

2

(AB+CD)•CE=

5 3

2

又∵PC⊥平面ABCD，CD?平面ABCD
∴PC⊥CD，Rt△PCD中，PC=

PD2-CD2

=

3

所以，根据锥体的体积公式，得V_P-ABCD=

1

3

S_ABCD•PC=

1

3

•

5 3

2

•

3

=

5

2

，
即此四棱锥的体积的体积为

5

2

．

点评：本题以底面为梯形、一条侧棱垂直于底的四棱锥为例，通过证明线线垂直和求体积，着重考查了空间垂直关系的证明与体积公式等知识点，属于中档题．