题目内容
证明下列三角恒等式：（1）
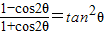；（2）
．
【答案】分析：（1）利用二倍角公式化简等式的左边 
=
，再利用同角三角函数的基本关系证得它等于
等式的右边．
（2）把等式的左边变形
=
，约分后分子分母同时除以cosθ，
即得等式的右边．
解答：证明：（1）等式的左边=
=
=
=tan2θ=右边，故等式成立．
（2）等式的左边=
=
=
=
=右边，故等式成立．
点评：本题考查二倍角公式、同角三角函数的基本关系，正确选择公式是解题的关键和难点．
=，再利用同角三角函数的基本关系证得它等于等式的右边．
（2）把等式的左边变形
=，约分后分子分母同时除以cosθ，即得等式的右边．
解答：证明：（1）等式的左边=
===tan2θ=右边，故等式成立．（2）等式的左边=
====右边，故等式成立．
点评：本题考查二倍角公式、同角三角函数的基本关系，正确选择公式是解题的关键和难点．
练习册系列答案
相关题目
；
．
.
.
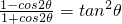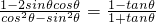