题目内容
已知集合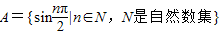 .
.(1)用列举法表示集合A;
(2)任取p∈A,q∈A,记向量
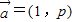 ,
,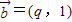 ,求
,求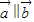 的概率.
的概率.
【答案】分析:(1)利用周期公式得出其周期,分别计算出函数值,即可得到集合A;
(2)分类讨论得出所以情况,再找出满足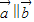 的基本事件,利用古典概型的概率计算公式即可得出.
的基本事件,利用古典概型的概率计算公式即可得出.
解答:解:(1)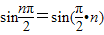 的周期为
的周期为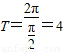 ,
,
n=0时,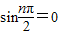 ;n=1时,
;n=1时,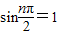 ;n=2时,
;n=2时,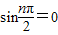 ;n=3时,
;n=3时,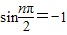
所以A={-1,0,1}.
(2)任取p∈A,q∈A,对应的向量分别有:①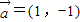 ,
,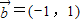 ,②
,②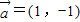 ,
,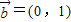 ,③
,③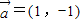 ,
,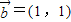 ,④
,④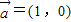 ,
,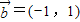 ,⑤
,⑤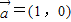 ,
,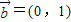 ,⑥
,⑥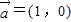 ,
,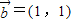 ,⑦
,⑦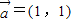 ,
,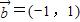 ,⑧
,⑧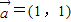 ,
,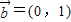 ,⑨
,⑨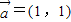 ,
,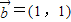 ,共9种情况.
,共9种情况.
其中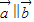 的情况分别是:①
的情况分别是:①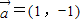 ,
,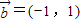 ,②
,②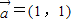 ,
,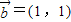 ,共2种情况.
,共2种情况.
由于各种不同情况是等可能的,故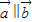 的概率
的概率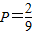 .
.
点评:熟练掌握周期公式、分类讨论、向量共线定理、古典概型的概率计算公式等是解题的关键.
(2)分类讨论得出所以情况,再找出满足
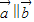 的基本事件,利用古典概型的概率计算公式即可得出.
的基本事件,利用古典概型的概率计算公式即可得出.解答:解:(1)
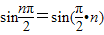 的周期为
的周期为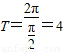 ,
,n=0时,
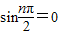 ;n=1时,
;n=1时,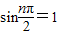 ;n=2时,
;n=2时,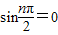 ;n=3时,
;n=3时,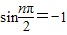
所以A={-1,0,1}.
(2)任取p∈A,q∈A,对应的向量分别有:①
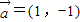 ,
,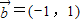 ,②
,②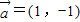 ,
,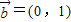 ,③
,③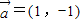 ,
,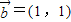 ,④
,④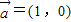 ,
,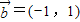 ,⑤
,⑤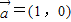 ,
,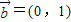 ,⑥
,⑥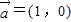 ,
,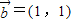 ,⑦
,⑦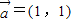 ,
,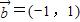 ,⑧
,⑧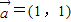 ,
,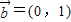 ,⑨
,⑨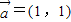 ,
,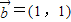 ,共9种情况.
,共9种情况.其中
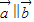 的情况分别是:①
的情况分别是:①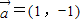 ,
,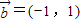 ,②
,②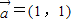 ,
,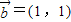 ,共2种情况.
,共2种情况.由于各种不同情况是等可能的,故
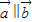 的概率
的概率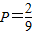 .
.点评:熟练掌握周期公式、分类讨论、向量共线定理、古典概型的概率计算公式等是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
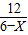 ∈N}用列举法表示集合A= .
∈N}用列举法表示集合A= . 。
。 ;(2)若
;(2)若 且
且 ,求实数
,求实数 的值。
的值。