题目内容
(本题满分为5分,计入总分,但总分不超过100分)
数列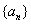 是以
是以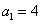 为首项的等比数列,且
为首项的等比数列,且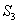 、
、 、
、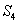 成等差数列. 设
成等差数列. 设 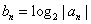 ,
,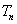 为数列
为数列 的前
的前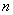 项和,若
项和,若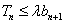 对一切
对一切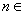 N*恒成立,求实数
N*恒成立,求实数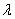 的最小值.
的最小值.
【答案】
解:当 时,
时, ,
, ,
, ,不成等差数列.
,不成等差数列.
当 时,
时, ,得
,得 ,所以
,所以 ,解得
,解得 .
.
所以 . (2分)
. (2分)
 ,
,
 .
.
所以 .
.
因为 ,所以
,所以 ,所以
,所以 .
.
又 .
.
当且仅当 时取等号,所以
时取等号,所以 的最小值为
的最小值为 . (5分)
. (5分)

练习册系列答案
相关题目
 ⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作
⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作 于E,求证:
于E,求证: .
. 
 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. 的值;
的值; 在区间
在区间 上的最大值;
上的最大值; ,曲线
,曲线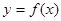 上是否存在两点
上是否存在两点 ,使得
,使得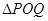 是以
是以 .
. 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.