Question

已知函数f（x）=mx+n的图象经过点A（1，2），B（-1，0），且函数h(x)=2p

x

（p＞0）与函数f（x）=mx+n的图象只有一个交点．
（1）求函数f（x）与h（x）的解析式；
（2）设函数F（x）=f（x）-h（x），求F（x）的最小值与单调区间；
（3）设a∈R，解关于x的方程log₄[f（x-1）-1]=log₂h（a-x）-log₂h（4-x）．

Answer 1

分析：（1）将点A（1，2），B（-1，0），坐标代入f（x）=mx+n可得函数f（x）的解析式，进而联立方程后根据函数h(x)=2p

x

（p＞0）与函数f（x）=mx+n的图象只有一个交点，根据二次方程根的个数与△的关系求出p值，得到h（x）的解析式；
（2）由（1）求出函数F（x）=f（x）-h（x）的解析式，结合二次函数的图象和性质可得F（x）的最小值与单调区间；
（3）原方程可化为：log₂（

4-x

•

x-1

）=log₂

a-x

，即

1＜x＜4 x＜a a=-(x-3)2+5

，根据二次函数的图象和性质分类讨论后综合讨论结果可得答案．

解答：解：（1）∵函数f（x）=mx+n的图象经过点A（1，2），B（-1，0），
∴

m+n=2 -m+n=0

解得：m=n=1
∴f（x）=x+1
由函数h(x)=2p

x

（p＞0）与函数f（x）=x+1的图象只有一个交点．
可得x-2p

x

+1=0有且只有一个解
即△=4p²-4=0，
又∵p＞0
∴p=1
∴h(x)=2

x

（2）由（1）得F（x）=f（x）-h（x）=x-2

x

+1=（

x

-1）²，
当

x

=1，即x=1时，F（x）_min=0．         …（6分）
F（x）在[0，1]为减函数，在[1，+∞）为增函数．   …（8分）
（3）原方程可化为：log₄（x-1）=log₂

a-x

-log₂

4-x

即

1

2

log₂（x-1）=log₂

a-x

-log₂

4-x

即

1

2

log₂（x-1）+log₂

4-x

=log₂（

4-x

•

x-1

）=log₂

a-x

即

x-1＞0 4-x＞0 a-x＞0 a-x=(x-1)(4-x)

即

1＜x＜4 x＜a a=-(x-3)2+5

…（10分）
令y═-（x-3）²+5

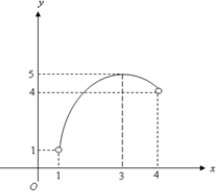
由上图可知：
①当1＜a≤4时，原方程有一解：x=3-

5-a

②当4＜a＜5时，原方程有两解：x=3-

5-a

，x=3+

5-a

，
③当a=5时，原方程有一解：x=3
④当a≤1或a＞5时，原方程无解

点评：本题考查的知识点是对数函数的图象和性质，二次函数的图象和性质，是函数图象和性质的综合应用，难度较大，属于难题．