题目内容
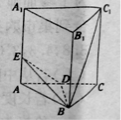
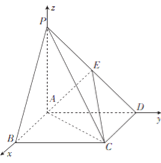
【题目】在如图所示的四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() .
.
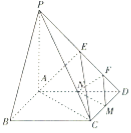
⑴证明:![]() 平面
平面![]() ;
;
⑵若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】⑴证明见解析;⑵![]() .
.
【解析】
试题分析:⑴做辅助线,由![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点
中点![]()
![]() .又
.又![]()
![]()
![]() 为
为![]() 中点,又
中点,又![]() ,
,![]()
![]()
![]() 为
为![]() 中点
中点![]()
![]()
![]()
![]()
![]()
![]() 平面
平面![]() ;⑵由
;⑵由![]() 平面
平面![]()
![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,求出平面
轴建立空间直角坐标系,求出平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的法向量为
的法向量为![]()
![]()
![]() . 由图可知,二面角
. 由图可知,二面角![]() 为钝角
为钝角![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
试题解析:⑴证明:连结![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连结
,连结![]() 、
、![]() ,
,
∵![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,∴
中点,∴![]() .……………………2分
.……………………2分
又![]() ,∴
,∴![]() 为
为![]() 中点,又
中点,又![]() ,
,![]() ,∴
,∴![]() 为
为![]() 中点,
中点,
∴![]() ,∴
,∴![]() .……………………………………4分
.……………………………………4分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .………………………………5分
.………………………………5分
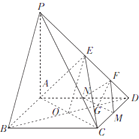
⑵解:∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .……………………………………6分
.……………………………………6分
如图 ,以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,
则![]() ,
,![]() ,………………………………7分
,………………………………7分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量
的一个法向量![]() .…………8分
.…………8分
设平面![]() 的法向量为
的法向量为![]() ,
,
则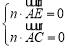 ,即
,即![]() ,…………………………9分
,…………………………9分
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,…………10分
,…………10分
∴![]() .……………………………………11分
.……………………………………11分
由图可知,二面角![]() 为钝角,
为钝角,
∴二面角![]() 的余弦值为
的余弦值为![]() .……………………………………12分
.……………………………………12分

练习册系列答案
相关题目
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
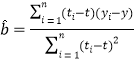 ,
,![]()