Question

若 x+2y+4z=1，则 x²+y²+z²的最小值是________．

Answer 1

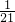
分析：x²+y²+z²的值可看作空间中的点（x，y，z）到原点的距离，这样的点在以原点为球心的球面上，x+2y+4z=1表示一个平面，x²+y²+z²的最小值是球与此平面相切时切点与原点的距离平方，即原点到此平面的距离的平方，由此 x²+y²+z²的最小值易求得
解答：由题意 x+2y+4z=1表示一个平面，x²+y²+z²的值表示空间中的点（x，y，z）到原点的距离，这样的点在以原点为球心的球面上，
∴x²+y²+z²的最小值是球与此平面相切时切点与原点的距离平方，即原点到此平面的距离的平方，
又原点到平面x+2y+4z=1的距离是d==
综上可得 x²+y²+z²的最小值是
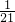
故答案为：．
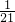点评：本题考查空间中点的坐标，解题的关键是理解x+2y+4z=1，与 x²+y²+z²的几何意义，利用几何意义将问题转化为点到面的距离求解，本题考查了数形结合与转化思想．