题目内容
求:(1)与双曲线x2-
=1有相同的渐近线,且过点(4,4)的双曲线.
(2)求(1)中双曲线的实轴长与虚轴长,离心率.
| y2 | 2 |
(2)求(1)中双曲线的实轴长与虚轴长,离心率.
分析:(1)设出与双曲线x2-
=1有相同的渐近线的双曲线方程为x2-
=λ,将(4,4)代入求得λ即可;
(2)由双曲线的标准方程结合双曲线的性质即可求得其实轴长与虚轴长,离心率.
| y2 |
| 2 |
| y2 |
| 2 |
(2)由双曲线的标准方程结合双曲线的性质即可求得其实轴长与虚轴长,离心率.
解答:解:(1)依题意,设所求的双曲线方程为x2-
=λ,
∵该双曲线过点(4,4),
∴λ=16-8=8,
∴所求的双曲线方程为
-
=1;
(2)∵双曲线方程为
-
=1,
∴实轴长为2a=4
,虚轴长为2b=8,离心率e=
=
=
.
| y2 |
| 2 |
∵该双曲线过点(4,4),
∴λ=16-8=8,
∴所求的双曲线方程为
| x2 |
| 8 |
| y2 |
| 16 |
(2)∵双曲线方程为
| x2 |
| 8 |
| y2 |
| 16 |
∴实轴长为2a=4
| 2 |
| c |
| a |
2
| ||
2
|
| 3 |
点评:本题考查双曲线的标准方程与双曲线的简单性质,考查待定系数法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
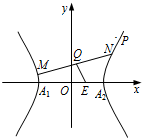 如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为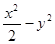 =1相交于两个不同的点A、B。
=1相交于两个不同的点A、B。 -y2=1相交于两个不同的点A、B.
-y2=1相交于两个不同的点A、B.