题目内容
(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)将 的图象向左平移
的图象向左平移 (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的图象上各最高点到点
的图象上各最高点到点 的距离的最小值为1,求
的距离的最小值为1,求 的单调增区间.
的单调增区间.
(I)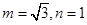 .
.
(II)函数 的单调递增区间为
的单调递增区间为 .
.
解析试题分析:(1)由题意知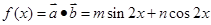 .
.
根据 的图象过点
的图象过点 和
和 ,得到
,得到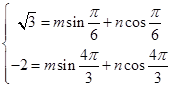 ,
,
解得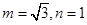 .
.
(2)由(1)知: .
.
由题意知: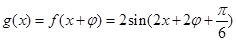 ,
,
依题意知到点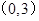 的距离为1的最高点为
的距离为1的最高点为 .
.
将其代入 得
得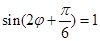 ,
,
可得 ,得到
,得到 ,
,
由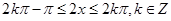 ,得
,得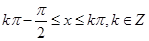 ,
,
得到 的单调递增区间为
的单调递增区间为 .
.
试题解析:(1)由题意知: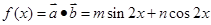 .
.
因为 的图象过点
的图象过点 和
和 ,
,
所以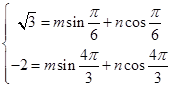 ,
,
即 ,
,
解得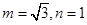 .
.
(2)由(1)知: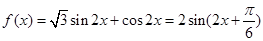 .
.
由题意知: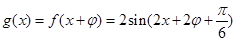 ,
,
设 的图象上符合题意的最高点为
的图象上符合题意的最高点为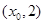 ,
,
由题意知: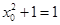 ,所以
,所以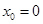 ,
,
即到点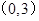 的距离为1的最高点为
的距离为1的最高点为 .
.
将其代入 得
得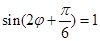 ,
,
因为 ,所以
,所以 ,
,
因此 ,
,
由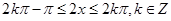 ,得
,得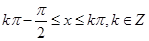 ,
,
所以,函数 的单调递增区间为
的单调递增区间为 .
.
考点:平面向量的数量积,三角函数的化简,三角函数的图象和性质.

练习册系列答案
相关题目
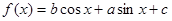 .
. 时,求
时,求 的值域;
的值域; ,
, 时,函数
时,函数 对称,求函数
对称,求函数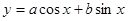 的对称轴;
的对称轴; ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得 的图象,又知
的图象,又知 的所有正根从小到大依次为
的所有正根从小到大依次为 ,
, ,…
,… ,…且
,…且 ,求
,求 的解析式.
的解析式. .
.
 的值域;
的值域; 的最大值和最小值.
的最大值和最小值. 的部分图象如图所示.
的部分图象如图所示. 的最小正周期及图中
的最小正周期及图中 、
、 的值;
的值;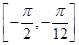 上的最大值和最小值.
上的最大值和最小值.
 ,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.
,边界AE,AF,EF的费用为每米1万元,区域内的费用为每平方米4 万元.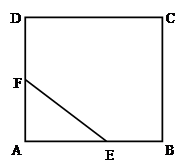
 )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.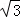 cos(x+π)cosx,(x∈R)
cos(x+π)cosx,(x∈R) =(
=( ,
,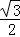 )平移后得到的函数y=g(x)的图象,求y=g(x)在(0,
)平移后得到的函数y=g(x)的图象,求y=g(x)在(0,