题目内容
已知函数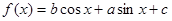 .
.
(1)当 时,求
时,求 的值域;
的值域;
(2)当 ,
, 时,函数
时,函数 的图象关于
的图象关于 对称,求函数
对称,求函数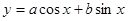 的对称轴;
的对称轴;
(3)若 图象上有一个最低点
图象上有一个最低点 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得 的图象,又知
的图象,又知 的所有正根从小到大依次为
的所有正根从小到大依次为 ,
, ,…
,… ,…且
,…且 ,求
,求 的解析式.
的解析式.
(1)①当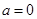 时,值域为:
时,值域为: ; ② 当
; ② 当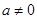 时,值域为:
时,值域为: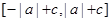 ;(2)
;(2)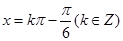 ;(3)
;(3)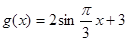
解析试题分析:(1)利用正弦函数的值域和不等式性质即可求出 的值域,主要要分
的值域,主要要分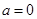 与
与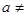 0两种情况;(2)先由对称轴过最值点列出关于
0两种情况;(2)先由对称轴过最值点列出关于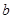 的方程,求出
的方程,求出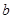 ,然后将函数
,然后将函数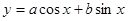 利用设辅助角公式化为一个角的三角函数,再利用求对称轴的方法求出对称轴;(3)先由设辅助角公式将函数
利用设辅助角公式化为一个角的三角函数,再利用求对称轴的方法求出对称轴;(3)先由设辅助角公式将函数 化成一个角的三角函数,利用
化成一个角的三角函数,利用 过最低点
过最低点 ,求出辅助角并将
,求出辅助角并将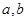 用
用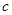 表示出来,即求出
表示出来,即求出 的解析式,再根据题中的图像变换求出
的解析式,再根据题中的图像变换求出 的解析式,再根据题中已知条件
的解析式,再根据题中已知条件 的所有正根从小到大依次为
的所有正根从小到大依次为 ,
, ,…
,… ,…且
,…且 确定参数
确定参数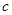 ,即可得到
,即可得到 的解析式.
的解析式.
试题解析:(1)当 时,
时,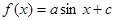
①当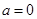 时,值域为:
时,值域为: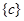 ② 当
② 当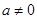 时,值域为:
时,值域为: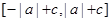
(2)当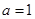 ,
, 时,
时,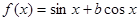 且图象关于
且图象关于 对称。
对称。
∴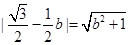
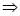
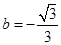 ∴函数
∴函数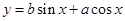 即:
即: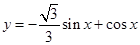 ∴
∴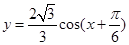 由
由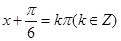
∴函数的对称轴为: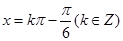
(3)由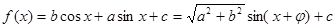
(其中 ,
,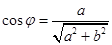 )
)
由 图象上有一个最低点
图象上有一个最低点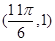 ,所以
,所以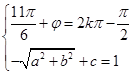
∴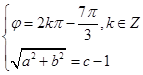 ∴
∴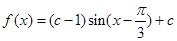
又图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得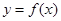 的图象,则
的图象,则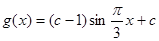
又∵ 的所有正根从小到大依次为
的所有正根从小到大依次为 ,
, ,…
,… ,…,且
,…,且
所以 与直线
与直线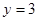 的相邻交点间的距离相等,根据三角函数的图象与性质可得以下情况:
的相邻交点间的距离相等,根据三角函数的图象与性质可得以下情况:
(1)直线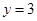 要么过
要么过 的最高点或最低点.
的最高点或最低点.
即 或
或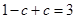 (矛盾),
(矛盾),
练习册系列答案
相关题目
 ,求
,求 的值
的值 的前n项和为
的前n项和为
 在
在 处取得最大值,且最大值为a2,求函数
处取得最大值,且最大值为a2,求函数 的解析式。
的解析式。
 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 ,求
,求 ,
, .
. 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值. ,
, .
. 的最小正周期;
的最小正周期; 上的值域.
上的值域.
 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 个单位,得到函数
个单位,得到函数 的图像,求
的图像,求 上的最大值和最小值,并求出相应的x的取值。
上的最大值和最小值,并求出相应的x的取值。 ,
, ,设函数
,设函数 ,且
,且 的图象过点
的图象过点 和点
和点 .
. 的值;
的值; (
( )个单位后得到函数
)个单位后得到函数 的图象.若
的图象.若 的距离的最小值为1,求
的距离的最小值为1,求 ),则sinx=______________.
),则sinx=______________.