题目内容
如图所示,已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=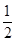 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).
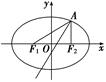
(1)求椭圆E的方程;
(2)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
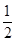 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).
(1)求椭圆E的方程;
(2)在椭圆E上是否存在关于直线l对称的相异两点?若存在,请找出;若不存在,说明理由.
(1) =1
=1
(2)不存在,见解析
 =1
=1(2)不存在,见解析
解:(1)设椭圆E的方程为 =1(a>b>0),
=1(a>b>0),
由题意e= =
=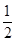 ,
, =1,
=1,
又∵c2=a2-b2,
解得:c=2,a=4,b=2 ,
,
∴椭圆E的方程为 =1.
=1.
(2)假设椭圆E上存在关于直线l对称的相异两点P、Q,令P(x1,y1)、Q(x2,y2),且PQ的中点为R(x0,y0).
∵PQ⊥l,
∴kPQ= =-
=-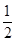 ,
,
又∵
两式相减得: .
.
∴ =-
=- =-
=- ×(-
×(-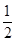 )=
)= ,
,
即 =
= ,③
,③
又∵R(x0,y0)在直线l上,
∴y0=2x0-1,④
由③④解得:x0=2,y0=3,
所以点R与点A是同一点,这与假设矛盾,
故椭圆E上不存在关于直线l对称的相异两点.
 =1(a>b>0),
=1(a>b>0),由题意e=
 =
=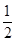 ,
, =1,
=1,又∵c2=a2-b2,
解得:c=2,a=4,b=2
 ,
,∴椭圆E的方程为
 =1.
=1.(2)假设椭圆E上存在关于直线l对称的相异两点P、Q,令P(x1,y1)、Q(x2,y2),且PQ的中点为R(x0,y0).
∵PQ⊥l,
∴kPQ=
 =-
=-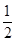 ,
,又∵

两式相减得:
 .
.∴
 =-
=- =-
=- ×(-
×(-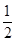 )=
)= ,
,即
 =
= ,③
,③又∵R(x0,y0)在直线l上,
∴y0=2x0-1,④
由③④解得:x0=2,y0=3,
所以点R与点A是同一点,这与假设矛盾,
故椭圆E上不存在关于直线l对称的相异两点.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
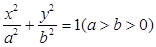 经过点
经过点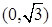 ,离心率为
,离心率为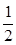 ,左右焦点分别为
,左右焦点分别为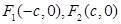 .
.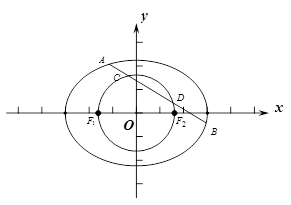
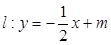 与椭圆交于
与椭圆交于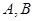 两点,与以
两点,与以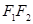 为直径的圆交于
为直径的圆交于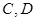 两点,且满足
两点,且满足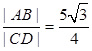 ,求直线
,求直线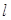 的方程.
的方程.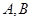 是抛物线
是抛物线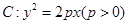 上不同的两点,点
上不同的两点,点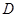 在抛物线
在抛物线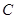 的准线
的准线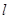 上,且焦点
上,且焦点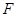 到直线
到直线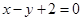 的距离为
的距离为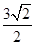 .
.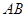 过焦点
过焦点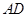 过原点
过原点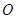 ;③直线
;③直线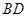 平行
平行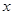 轴.
轴.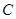 :
: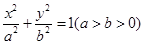 的右焦点为
的右焦点为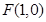 ,短轴的一个端点
,短轴的一个端点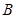 到
到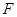 的距离等于焦距.
的距离等于焦距.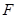 的直线
的直线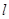 与椭圆
与椭圆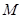 ,
,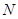 ,是否存在直线
,是否存在直线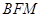 与△
与△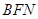 的面积比值为
的面积比值为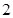 ?若存在,求出直线
?若存在,求出直线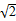 的圆C与直线y=x相切于坐标原点O,椭圆
的圆C与直线y=x相切于坐标原点O,椭圆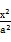 +
+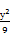 =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10.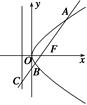
 x
x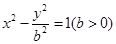 的一条渐近线与圆
的一条渐近线与圆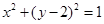 至多有一个交点,则双曲线离心
至多有一个交点,则双曲线离心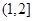
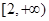
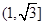
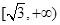
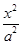 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.