题目内容
正四棱柱ABCD-A1B1C1D1的底面边长为2
,AA1=2,点M是BC的中点,P是平面A1BCD1内的一个动点,且满足PM≤2,P到A1D1和AD的距离相等,则点P的轨迹的长度为( )
| 2 |
分析:由题意画出几何体的图形,判断满足椭圆的点P的位置是图中线段EF,求出EF的长度即可.
解答: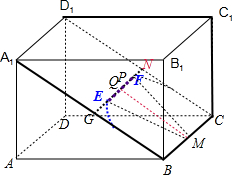 解:∵正四棱柱ABCD-A1B1C1D1的底面边长为2
解:∵正四棱柱ABCD-A1B1C1D1的底面边长为2
,AA1=2,
点M是BC的中点,P是平面A1BCD1内的一个动点,
且满足PM≤2,P到A1D1和AD的距离相等,
如图,P在平面A1D1CB中GN(G是A1B的中点,N是D1C的中点)的线段EF,
满足GE=FN=
-1,Q为GN的中点,QM=
BA1=
×
=
,ME=2,
所以EQ=
=1,同理QF=1,
所以EF=2,
∴点P的轨迹的长度为2.
故选D.
 解:∵正四棱柱ABCD-A1B1C1D1的底面边长为2
解:∵正四棱柱ABCD-A1B1C1D1的底面边长为2| 2 |
点M是BC的中点,P是平面A1BCD1内的一个动点,
且满足PM≤2,P到A1D1和AD的距离相等,
如图,P在平面A1D1CB中GN(G是A1B的中点,N是D1C的中点)的线段EF,
满足GE=FN=
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
22+(2
|
| 3 |
所以EQ=
22-(
|
所以EF=2,
∴点P的轨迹的长度为2.
故选D.
点评:本题考查点线面间距离的计算,解题时要认真审题,仔细解答,注意化空间问题为平面问题.考查空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
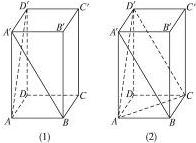 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是