题目内容
已知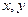 满足不等式组
满足不等式组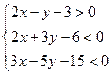 ,求使
,求使
 取最大值的整数
取最大值的整数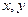 .
.
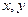 满足不等式组
满足不等式组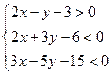 ,求使
,求使
 取最大值的整数
取最大值的整数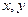 .
. 最大整数解为
最大整数解为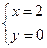 或
或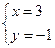
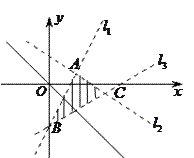
先作平面区域,再作一组平行线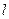 :
: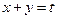 平行于
平行于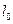 :
: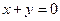
进一步寻找整点.
不等式组的解集为三直线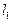 :
: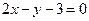 ,
,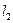 :
: ,
,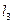 :
: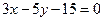 所围成的三角形内部(不含边界),设
所围成的三角形内部(不含边界),设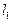 与
与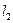 ,
,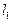 与
与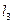 ,
,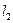 与
与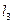 交点分别为
交点分别为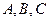 ,则
,则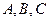 坐标分别为
坐标分别为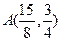 ,
,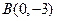 ,
,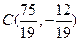 ,
,
作一组平行线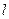 :
: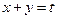 平行于
平行于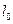 :
: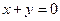 ,
,
当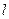 往
往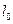 右上方移动时,
右上方移动时,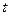 随之增大,
随之增大,
∴当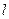 过
过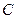 点时
点时 最大为
最大为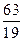 ,但不是整数解,
,但不是整数解,
又由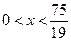 知
知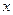 可取
可取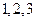 ,
,
当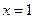 时,代入原不等式组得
时,代入原不等式组得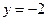 , ∴
, ∴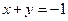 ;
;
当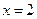 时,得
时,得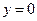 或
或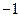 , ∴
, ∴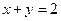 或
或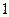 ;
;
当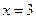 时,
时,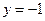 , ∴
, ∴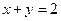 ,故
,故
 的最大整数解为
的最大整数解为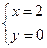 或
或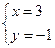 .
.
【名师指引】在平行域内找整点最优解,一般采用平移找解法,即打网格,描整点,平移直线,找出最优解
 :
: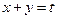 平行于
平行于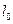 :
: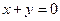
进一步寻找整点.
不等式组的解集为三直线
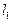 :
: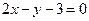 ,
,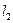 :
: ,
,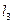 :
: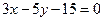 所围成的三角形内部(不含边界),设
所围成的三角形内部(不含边界),设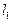 与
与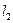 ,
,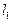 与
与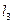 ,
,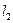 与
与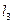 交点分别为
交点分别为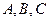 ,则
,则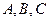 坐标分别为
坐标分别为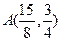 ,
,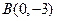 ,
,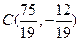 ,
,作一组平行线
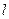 :
: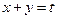 平行于
平行于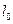 :
: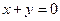 ,
,当
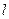 往
往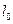 右上方移动时,
右上方移动时,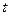 随之增大,
随之增大,∴当
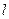 过
过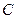 点时
点时 最大为
最大为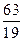 ,但不是整数解,
,但不是整数解,又由
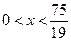 知
知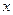 可取
可取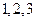 ,
,当
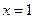 时,代入原不等式组得
时,代入原不等式组得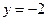 , ∴
, ∴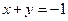 ;
;当
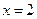 时,得
时,得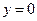 或
或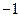 , ∴
, ∴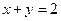 或
或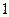 ;
;当
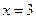 时,
时,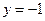 , ∴
, ∴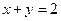 ,故
,故
 的最大整数解为
的最大整数解为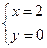 或
或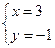 .
.【名师指引】在平行域内找整点最优解,一般采用平移找解法,即打网格,描整点,平移直线,找出最优解

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
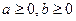 ,且当
,且当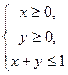 时,恒有
时,恒有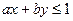 ,则以
,则以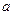 ,b为坐标点P(
,b为坐标点P( 则
则 的最小值是( ).
的最小值是( ).



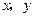 满足约束条件:
满足约束条件: ,则
,则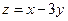 的最小值( )
的最小值( )



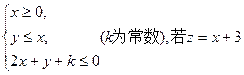 y的最大值为8,则
y的最大值为8,则 .
. 、
、 满足约束条件
满足约束条件 ,则z=2x+3y的最大值为
,则z=2x+3y的最大值为 


 ,若目标函数
,若目标函数 (其中
(其中 >0),仅在(4,2)处取得最大值,则
>0),仅在(4,2)处取得最大值,则 则z的最大值为( )
则z的最大值为( )
