题目内容
已知平面上一定点C(-1,0)和一直线l:x=-4,P(x,y)为该平面上一动点,作PQ⊥l,垂足为Q,且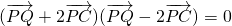 .
.
(1)求点P的轨迹方程;
(2)点O是坐标原点,过点C的直线与点P的轨迹交于A,B两点,求 的取值范围.
的取值范围.
解:(1)设P(x,y),则由已知得Q(-4,y),又C(-1,0),
∴ =(-4-x,0),
=(-4-x,0), =(-1-x,-y),
=(-1-x,-y),
∵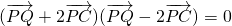 .
.
∴(-6-3x,-2y)•(-2+x,2y)=0,
故 .
.
(2)设过点C的直线斜率存在时的方程为y=k(x+1),A(x1,y1),B(x2,y2)
则由 ?(3+4k2)x2+8k2x+4k2-12=0
?(3+4k2)x2+8k2x+4k2-12=0
∴ ,
,
 ,
,
令
=
∵k2≥0,
∴
∴
当过点C的直线斜率不存在时,其方程为x=-1,解得
此时 ,
,
所以 的范围是
的范围是
分析:(1)设P(x,y),由题意可得Q(-4,y),又C(-1,0),结合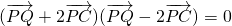 即可求得点P的轨迹方程;
即可求得点P的轨迹方程;
(2)设过点C的直线斜率存在时的方程为y=k(x+1),A(x1,y1),B(x2,y2)由 可得:(3+4k2)x2+8k2x+4k2-12=0,利用韦达定理,
可得:(3+4k2)x2+8k2x+4k2-12=0,利用韦达定理, 可化为:
可化为: ,从而可求其取值范围;当过点C的直线斜率不存在时可解得A、B两点的坐标从而可补充前者所求的
,从而可求其取值范围;当过点C的直线斜率不存在时可解得A、B两点的坐标从而可补充前者所求的 的取值范围.
的取值范围.
点评:本题考查直线与圆锥曲线的综合问题,考查向量在几何中的应用,突出方程思想,转化思想的考查与运用,属于难题.
∴
 =(-4-x,0),
=(-4-x,0), =(-1-x,-y),
=(-1-x,-y),∵
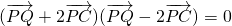 .
.∴(-6-3x,-2y)•(-2+x,2y)=0,
故
 .
.(2)设过点C的直线斜率存在时的方程为y=k(x+1),A(x1,y1),B(x2,y2)
则由
 ?(3+4k2)x2+8k2x+4k2-12=0
?(3+4k2)x2+8k2x+4k2-12=0∴
 ,
, ,
,令

=

∵k2≥0,
∴

∴

当过点C的直线斜率不存在时,其方程为x=-1,解得

此时
 ,
,所以
 的范围是
的范围是
分析:(1)设P(x,y),由题意可得Q(-4,y),又C(-1,0),结合
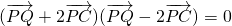 即可求得点P的轨迹方程;
即可求得点P的轨迹方程;(2)设过点C的直线斜率存在时的方程为y=k(x+1),A(x1,y1),B(x2,y2)由
 可得:(3+4k2)x2+8k2x+4k2-12=0,利用韦达定理,
可得:(3+4k2)x2+8k2x+4k2-12=0,利用韦达定理, 可化为:
可化为: ,从而可求其取值范围;当过点C的直线斜率不存在时可解得A、B两点的坐标从而可补充前者所求的
,从而可求其取值范围;当过点C的直线斜率不存在时可解得A、B两点的坐标从而可补充前者所求的 的取值范围.
的取值范围.点评:本题考查直线与圆锥曲线的综合问题,考查向量在几何中的应用,突出方程思想,转化思想的考查与运用,属于难题.

练习册系列答案
相关题目