题目内容
设函数![]() 的定义域为R,当
的定义域为R,当![]() ,且对任意的实数x,y∈R,有
,且对任意的实数x,y∈R,有![]() .
.
(I)求f(0),判断并证明函数![]() 的单调性;
的单调性;
(II)数列![]() N*).
N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 对于n不少于2的正整数恒成立,求x的取值范围.
对于n不少于2的正整数恒成立,求x的取值范围.
解:(I)令![]()
![]()
![]()
任取![]()
![]()
![]() 上是减函数.
上是减函数.
(II)(1)![]()
∴![]() 的单调性得
的单调性得![]() 是公差为2的等差数列,
是公差为2的等差数列,
![]()
(2)记![]() ,
,
![]()
![]() 是递增数列.
是递增数列.

故x的取值范围是![]()

练习册系列答案
相关题目
设函数 的定义域为R+,若对于给定的正数K,定义函数
的定义域为R+,若对于给定的正数K,定义函数 ,则当函数
,则当函数 时,定积分
时,定积分 的值为
的值为
( )
| A.2ln2+2 | B.2ln2-1 | C.2ln2 | D.2ln2+1 |
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
 的值;
的值; 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值. 的定义域为R,如果存在函数
的定义域为R,如果存在函数 为常数),使得
为常数),使得 对于一切实数
对于一切实数 都成立,那么称
都成立,那么称 为函数
为函数 ,
, 是函数
是函数 的一个承托函数,记实数a的取值范围为集合M,则有( )A.
的一个承托函数,记实数a的取值范围为集合M,则有( )A. 



 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 ,
, ,有
,有
 ; (2)试判断函数
; (2)试判断函数 在
在 上是否存在最大值,若存在,求出该最大值,若不存在说明理由;
上是否存在最大值,若存在,求出该最大值,若不存在说明理由; 各项都是正数,且满足
各项都是正数,且满足
 ,又设
,又设 ,
, ,试比较
,试比较 与
与  的大小.
的大小.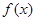 的定义域为R,且
的定义域为R,且

 的取值范围是 ( )
的取值范围是 ( )  B.(
B.(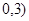 C.(
C.( D.
D.