a,b∈R.证明 -≤|a-b|. 题目和参考答案——青夏教育精英家教网——

题目内容

a,b∈R，证明 -≤|a-b|.

分析：本题的证法较多，整理谈谈如何利用“函数y=f(x)图象上任意两点P(x₁,y₁)，Q(x₂,y₂)连线的斜率k=y₁-y₂x₁-x₂(x₁≠x₂)的取值范围，就是曲线上任一点切线的斜率（如果有的话）的范围.”这一结论来证明.?

若a=b时，不等式是显然成立；

若a≠b时，原不等式等价于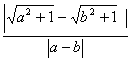≤1.不妨设f(x)=,

P(a,),Q（b,）(a≠b)则问题转化为：在函数f(x)=的图象上任取两点P,Q，求直线PQ的斜率的范围.

因为函数y=f(x)的图象上任意两点连线的斜率的范围，就是曲线上任一点切线斜率的范围.因此将问题进一步转化为：求y=f(x)的导数f′(x)的值域的问题.这样，问题便轻松获解.

∵f′(x)=,

∴|f′(x)|=||＜||=1.

∴||＜1,

即|f(x₁)-f(x₂)|＜|x₁-x₂|,综合得原不等式成立.

练习册系列答案

中考指要系列答案

金牌1号名优测试卷系列答案

培生新课堂同步训练与单元测评系列答案

中考系列红十套系列答案

中考新方向系列答案

中考新航线系列答案

专项新评价中考二轮系列答案

中考研究全国各省市中考真题常考基础题系列答案

中考通系列答案

中考添翼中考总复习系列答案

相关题目

已知f（x）是R上的增函数，a，b∈R．证明下面两个命题：
（1）若a+b＞0，则f（a）+f（b）＞f（-a）+f（-b）；
（2）若f（a）+f（b）＞f（-a）+f（-b），则a+b＞0．

已知函数f（x）是R上的增函数，a，b∈R，证明：若f（a）+f（b）＞f（-a）+f（-b），则a+b＞0．

已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R，对命题“若a+b≥0,则f(a)+f(b)≥f(-a)+f(-b)”.

(1)写出其逆命题，判断其真假，并证明你的结论;

(2)写出其逆否命题，判断其真假，并证明你的结论.

已知函数y=f(x)的定义域为R，且对任意a,b∈R,都有f(a+b)=f(a)+f(b)，且当x＞0时，f(x)＜0恒成立，f(3)=-3.

(1)证明：函数y=f(x)是R上的减函数；

（2）证明：函数y=f(x)是奇函数；

（3）试求函数y=f(x)在［m,n］（m,n∈Z）上的值域.