题目内容
已知a=(cosx+sinx,sinx),b=(cosx-sinx,2cosx),设f(x)=a·b.
(1)求函数f(x)的最小正周期;
(2)当x∈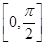 时,求函数f(x)的最大值和最小值.
时,求函数f(x)的最大值和最小值.
(1)求函数f(x)的最小正周期;
(2)当x∈
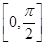 时,求函数f(x)的最大值和最小值.
时,求函数f(x)的最大值和最小值.(1)T=π(2)最小值-1,最大值

(1)f(x)=a·b
=(cosx+sinx)·(cosx-sinx)+sinx·2cosx=cos2x-sin2x+2sinxcosx
=cos2x+sin2x= =
= sin
sin .
.
∴f(x)的最小正周期T=π.
(2)∵0≤x≤ ,∴
,∴ ≤2x+
≤2x+ ≤
≤ ,
,
∴当2x+ =
= ,即x=
,即x= 时,f(x)有最大值
时,f(x)有最大值 ;当2x+
;当2x+ =
= ,即x=
,即x= 时,f(x)有最小值-1.
时,f(x)有最小值-1.
=(cosx+sinx)·(cosx-sinx)+sinx·2cosx=cos2x-sin2x+2sinxcosx
=cos2x+sin2x=
 =
= sin
sin .
.∴f(x)的最小正周期T=π.
(2)∵0≤x≤
 ,∴
,∴ ≤2x+
≤2x+ ≤
≤ ,
,∴当2x+
 =
= ,即x=
,即x= 时,f(x)有最大值
时,f(x)有最大值 ;当2x+
;当2x+ =
= ,即x=
,即x= 时,f(x)有最小值-1.
时,f(x)有最小值-1.
练习册系列答案
相关题目
 、
、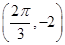 ,则这个函数的解析式为________.
,则这个函数的解析式为________.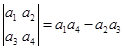 将函数
将函数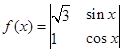 的图像向左平移
的图像向左平移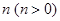 个单位,所得图像对应的函数为偶函数,则
个单位,所得图像对应的函数为偶函数,则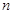 的最小值为( )
的最小值为( )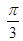
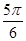
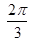
 sinxcosx+cos2x+a.
sinxcosx+cos2x+a. 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 ,求a的值.
,求a的值.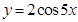 的图像,只需将函数
的图像,只需将函数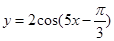 的图像( )
的图像( )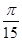 个单位
个单位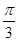 个单位
个单位 ,则f(
,则f( )=( )
)=( )