题目内容
函数f（x）=x（m-x）满足f（2-x）=f（x），且在区间[a，b]上的值域是[-3，1]，则坐标（a，b）所表示的点在图中的（ ）| A、线段AD和线段BC上 | B、线段AD和线段DC上 | C、线段AB和线段DC上 | D、线段AC和线段BD上 |
分析：先根据图象的对称性求得f（x）=x（2-x），由题意可得-1≤a≤1，1≤b≤3．且当a=-1时，1≤b≤3；-1＜a≤1时，b=3，由此可得答案．
解答：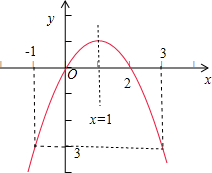
解：∵函数f（x）=x（m-x）满足f（2-x）=f（x），
故函数的图象关于直线x=1对称，且开口向上，
所以，m=2，f（x）=x（2-x）．
再根据f（-1）=-3=f（3），f（1）=1，画出函数f（x）的图象，
如图所示．
故有-1≤a≤1，1≤b≤3．
且当a=-1时，1≤b≤3；-1＜a≤1时，b=3，
故坐标（a，b）所表示的点在图中的线段AD和线段DC上，
故选：B．
解：∵函数f（x）=x（m-x）满足f（2-x）=f（x），故函数的图象关于直线x=1对称，且开口向上，
所以，m=2，f（x）=x（2-x）．
再根据f（-1）=-3=f（3），f（1）=1，画出函数f（x）的图象，
如图所示．
故有-1≤a≤1，1≤b≤3．
且当a=-1时，1≤b≤3；-1＜a≤1时，b=3，
故坐标（a，b）所表示的点在图中的线段AD和线段DC上，
故选：B．
点评：本题主要考查函数的图象特征，注意（a，b）的取值范围，属于基础题．
练习册系列答案
相关题目