题目内容
已知函数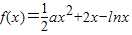
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间
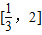 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
【答案】分析:(1)因为当函数的导数为0时,函数有极值,所以当a=0时,必须先在定义域中求函数f(x)的导数,让导数等于0,求x的值,得到极值点,在列表判断极值点两侧导数的正负,根据所列表,判断何时有极值.
(2)因为当函数为增函数时,导数大于0,若f(x)在区间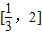 上是增函数,则f(x)在区间
上是增函数,则f(x)在区间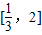 上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间
上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间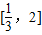 上恒大于0即可.
上恒大于0即可.
解答:解:(1)函数的定义域为(0,+∞)
∵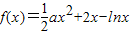 当a=0时,f(x)=2x-lnx,则
当a=0时,f(x)=2x-lnx,则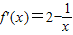
∴x,f'(x),f(x)的变化情况如下表
∴当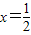 时,f(x)的极小值为1+ln2,函数无极大值.
时,f(x)的极小值为1+ln2,函数无极大值.
(2)由已知,得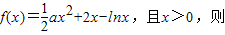
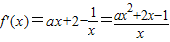
若a=0,由f'(x)>0得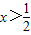 ,显然不合题意
,显然不合题意
若a≠0∵函数f(x)区间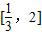 是增函数
是增函数
∴f'(x)≥0对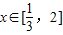 恒成立,即不等式ax2+2x-1≥0对
恒成立,即不等式ax2+2x-1≥0对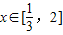 恒成立
恒成立
即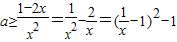 恒成立 故
恒成立 故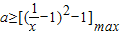
而当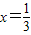 ,函数
,函数 ,∴实数a的取值范围为a≥3.
,∴实数a的取值范围为a≥3.
点评:本题考查了利用导数求函数极值以及函数单调性,属于常规题,必须掌握.
(2)因为当函数为增函数时,导数大于0,若f(x)在区间
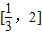 上是增函数,则f(x)在区间
上是增函数,则f(x)在区间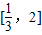 上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间
上恒大于0,所以只需用(1)中所求导数,令导数大于0,再判断所得不等式当a为何值时,在区间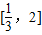 上恒大于0即可.
上恒大于0即可.解答:解:(1)函数的定义域为(0,+∞)
∵
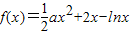 当a=0时,f(x)=2x-lnx,则
当a=0时,f(x)=2x-lnx,则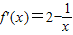
∴x,f'(x),f(x)的变化情况如下表
| x | (0, ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | - | + | |
| f(x) | 极小值 |
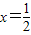 时,f(x)的极小值为1+ln2,函数无极大值.
时,f(x)的极小值为1+ln2,函数无极大值.(2)由已知,得
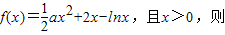
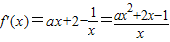
若a=0,由f'(x)>0得
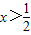 ,显然不合题意
,显然不合题意若a≠0∵函数f(x)区间
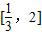 是增函数
是增函数∴f'(x)≥0对
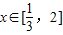 恒成立,即不等式ax2+2x-1≥0对
恒成立,即不等式ax2+2x-1≥0对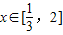 恒成立
恒成立即
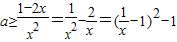 恒成立 故
恒成立 故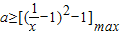
而当
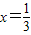 ,函数
,函数 ,∴实数a的取值范围为a≥3.
,∴实数a的取值范围为a≥3.点评:本题考查了利用导数求函数极值以及函数单调性,属于常规题,必须掌握.

练习册系列答案
相关题目
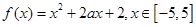
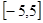 上是单调函数
上是单调函数 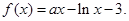
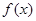 在点(1,-2)处的切线方程;
在点(1,-2)处的切线方程;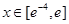 上的图象与直线
上的图象与直线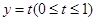 总有两个不同交点,求实数a的取值范围。
总有两个不同交点,求实数a的取值范围。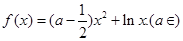
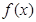 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;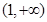 上,函数
上,函数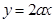 下方,求a的取值范围。
下方,求a的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。
 的图象与直线y=ax只有一个公共点,求实数b的取值范围。
的图象与直线y=ax只有一个公共点,求实数b的取值范围。