Question

（2007•潍坊二模）如图中心在原点，焦点在x轴上的椭圆，离心率e=

2

2

，且经过抛物线x²=4y的焦点．
（I）求椭圆的标准方程；
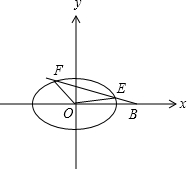
（Ⅱ）若过点B（2，0）的直线l（斜率不等于零）与椭圆交于不同的两点E、F（E在B、F之间），试求△OBE与△OBF面积之比的取值范围．

Answer 1

分析：（Ⅰ）求出抛物线的焦点坐标，根据椭圆中心在原点，焦点在x轴上求得b的值，再由椭圆的离心率求出a与c的关系，结合b²=a²-c²求出a²，从而椭圆的方程可求；
（Ⅱ）点B在椭圆之外，由图形可知当线段趋近椭圆切线时，E和F点也趋近重合，此时

S△OBE

S△OBF

趋近于1，当E、F点趋近X轴时三角形OBE和三角形OBF面积之比则趋近

OB-a

OB+a

=

2- 2

2+ 2

=3-2

2

．则答案可求．

解答：解：（1）抛物线x²=4y的焦点为（0，1），而椭圆经过其焦点，又长轴在X轴上，
则短半轴长为1，
设椭圆方程为

x2

a2

+

y2

b2

=1．
由b=1，e=

c

a

=

2

2

，c=

2 a

2

．
b2=a2-c2=a2-

a2

2

=

a2

2

=1，
所以a²=2，
故椭圆方程为：

x2

2

+y2=1；
（2）如图，点B坐标（2，0）在椭圆之外，当线段趋近椭圆切线时，E和F点也趋近重合，
此时

S△OBE

S△OBF

趋近于1，
而当E、F点趋近X轴时三角形OBE和三角形OBF面积之比则趋近

OB-a

OB+a

=

2- 2

2+ 2

=3-2

2

．
故3-2

2

＜

S△OBE

S△OBF

＜1．

点评：本题考查了椭圆的方程，考查了直线和圆锥曲线的关系，考查了数形结合的解题思想和极限思想，是有一定难度题目．