题目内容
【题目】已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 且
且![]() ,
,![]() ,数列
,数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设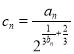 ,求
,求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)证明:对一切![]() ,
,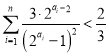
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)当![]() 时,构造
时,构造![]() ,变形为
,变形为![]() ,再求数列的通项公式;
,再求数列的通项公式;
(2)由已知变形为![]() ,利用累加法求数列
,利用累加法求数列![]() 的通项公式,然后再求数列
的通项公式,然后再求数列![]() 的通项公式,利用错位相减法求和;
的通项公式,利用错位相减法求和;
(3)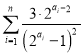 表示求数列
表示求数列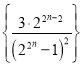 的前
的前![]() 项和,然后将通项放缩为
项和,然后将通项放缩为![]() 时,
时,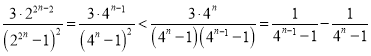 ,然后利用裂项相消法求和.
,然后利用裂项相消法求和.
(1)![]() 时,可得
时,可得![]() ,
,
![]() 时,
时,![]() ,
,![]() ,两式相减,
,两式相减,
得![]() ,
,![]() ,
,
![]() ,
,
![]() 数列
数列![]() 的奇数项和偶数项分别成以4为公差的等差数列,
的奇数项和偶数项分别成以4为公差的等差数列,
当![]() ,
,![]() 时,
时,![]() ,
,
当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,
,![]() .
.
(2)![]()
![]() ,
,
![]() ,即
,即![]() ,
,
整理为:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…………………………,
![]() ,
,![]() 时,
时,
这![]() 个式子相加可得
个式子相加可得![]() ,
,
![]() ,当
,当![]() 时,
时,![]() 成立,
成立,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
两式相减可得:![]()
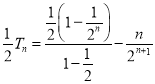 ,
,
![]()
(3)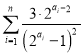 表示求数列
表示求数列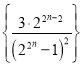 的前
的前![]() 项和,设前
项和,设前![]() 项和为
项和为![]() ,
,
当![]() 时,
时,![]() 成立,
成立,
当![]() 时,
时,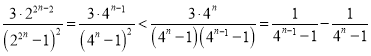
![]()
![]() .
.
综上可知![]() ,
,
![]() 对一切
对一切![]() ,
,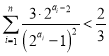 .
.

练习册系列答案
相关题目