题目内容
如果sinx+cosx=-
，且0＜x＜π，那么cotx的值是（ ）A．-
B．-
或-
C．-
D．
或-
【答案】分析：用已知的等式表示出sinx，代入sin2x+cos2x=1中，求出cosx的值，进而确定出sinx的值，再利用同角三角函数间的基本关系即可求出cotx的值．
解答：解：由sinx+cosx=-
，得到sinx=-（cosx+
），
代入sin2x+cos2x=1得：（cosx+
）2+cos2x=1，
即（5cosx+4）（5cosx-3）=0，
∴cosx=-
或cosx=
，
∵0＜x＜π，∴sinx＞0，故cosx=
舍去，
∴sinx=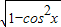
=
=
，
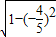则cotx=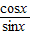
=-
．
故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
解答：解：由sinx+cosx=-
，得到sinx=-（cosx+），代入sin2x+cos2x=1得：（cosx+
）2+cos2x=1，即（5cosx+4）（5cosx-3）=0，
∴cosx=-
或cosx=，∵0＜x＜π，∴sinx＞0，故cosx=
舍去，∴sinx=
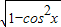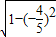==，则cotx=
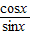=-．故选A
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目