题目内容
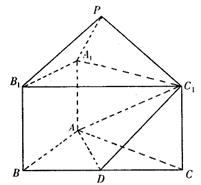
如图,底面△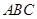 为正三角形的直三棱柱
为正三角形的直三棱柱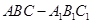 中,
中,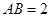 ,
,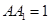 ,
, 是
是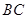 的中点,点
的中点,点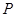 在平面
在平面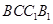 内,
内, .
. 
(Ⅰ)求证: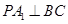 ;
;
(Ⅱ)求证: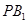 ∥平面
∥平面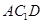 ;
;
(Ⅲ)求二面角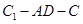 的大小.
的大小.
(Ⅰ)利用线面垂直证明线线垂直.(Ⅱ)线线平行证明线面平行.(Ⅲ)  .
.
解析试题分析:(Ⅰ)取 的中点
的中点 ,连结
,连结 ,
, ,
,
∴ ,
,  .
.
又 ,
, ,
, ,
,
∴ 平面
平面 .
.
又 ,∴
,∴ .
.
∵ ,∴
,∴ .
.
(Ⅱ)连结 ,在
,在 中,
中, ,
, ,
, 为中点,
为中点,
∴ ,
, .
.
∴ ,∴四边形
,∴四边形 为平行四边形.∴
为平行四边形.∴ .
.
又 ,∴
,∴ .
.
又∵ 面
面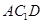 ,∴
,∴ 平面
平面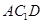 .
.
(Ⅲ)二面角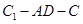 的大小为
的大小为 .
.
考点:本题考查了空间中的线面关系
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理

练习册系列答案
相关题目
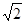 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.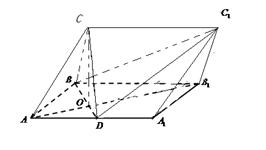
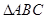 中,
中, 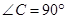 ,
,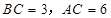 .D、E分别是
.D、E分别是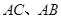 上的点,且
上的点,且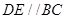 .将
.将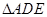 沿
沿 折起到
折起到 的位置,使
的位置,使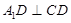 ,如图2.
,如图2.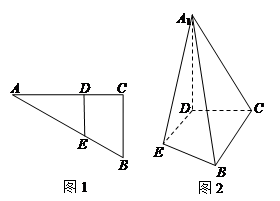
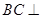 平面
平面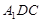 ;
;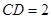 ,求
,求 与平面
与平面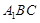 所成角的正弦值;
所成角的正弦值;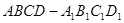 中,底面
中,底面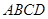 是正方形,
是正方形,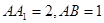 ,
, 是
是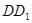 上的一点.
上的一点.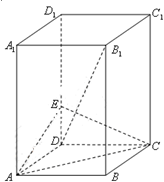
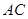 与
与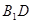 所成的角;
所成的角;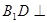 平面
平面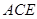 ,求三棱锥
,求三棱锥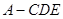 的体积;
的体积;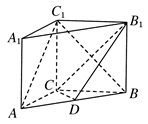
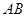 为圆
为圆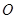 的直径,点
的直径,点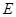 、
、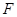 在圆
在圆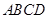 所在的平面和圆
所在的平面和圆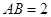 ,
,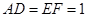 .
.
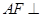 平面
平面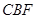 ;
;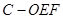 的体积.
的体积.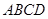 中,
中,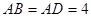 ,
,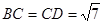 ,点
,点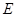 为线段
为线段 上的一点.现将
上的一点.现将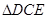 沿线段
沿线段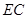 翻折到
翻折到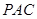 (点
(点 与点
与点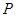 重合),使得平面
重合),使得平面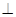 平面
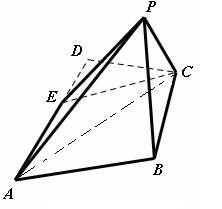
平面 ,连接
,连接 ,
, .
.
 平面
平面 ,且点
,且点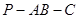 的大小.
的大小.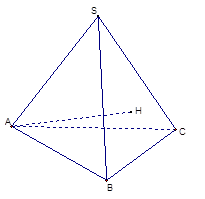
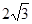 ,求三棱锥S—ABC的体积.
,求三棱锥S—ABC的体积.