题目内容
已知四棱锥P—ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=(1)若k=![]() 时,试判断PD与平面AMC的位置关系,并给予证明;
时,试判断PD与平面AMC的位置关系,并给予证明;
(2)k为何值时,二面角A-MC-B大小为![]() ?
?
解:(1)PD∥平面AMC.?
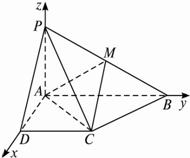
以AD,AB,AP为x,y,z轴建立如图坐标系,则P(0,0,1),C(1,1,0),B(0,2,0),D(1,0,0),M(0, ![]() ,
,![]() ). ?
). ?
∴![]() =(-1,0,1),
=(-1,0,1),![]() =(0,
=(0,![]() ,
,![]() ),
),![]() =(-1,-
=(-1,-![]() ,
,![]() ). ?
). ?
![]() =λ
=λ![]() +μ
+μ![]() ,?
,?
∴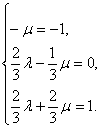 ?
?
∴λ=![]() ,μ=1. ?
,μ=1. ?
![]() =
=![]()
![]() +
+![]() ,∴DP∥平面AMC. ?
,∴DP∥平面AMC. ?

(2)设平面AMC的法向量n1=(a,b,1),平面MCB的法向量为n2=(c,d,1).?
M(0,2k,1-k),![]() =(1,1,0),
=(1,1,0),![]() =(0,2k,1-k),
=(0,2k,1-k),![]() =(1,-1,0),
=(1,-1,0),![]() =(0,2,-1).?
=(0,2,-1).?
∴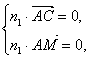 ∴
∴![]() ∴
∴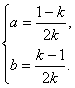
∴n1=(![]() ,
,![]() ,1). ?
,1). ?
∴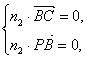 ∴
∴![]() ∴
∴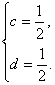 ∴n2=(
∴n2=(![]() ,
,![]() ,1). ?
,1). ?
若二面角AMCB的大小为![]() ,?
,?
则cos〈n1,n2〉=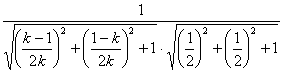 =
=![]() ,?
,?
∴(![]() +1)×
+1)×![]() =2.?
=2.?
∴![]() =
=![]() .?
.?
∴k2-6k+3=0.?
∴k=3±![]() (∵0≤k≤1,∴3+6舍去).?
(∵0≤k≤1,∴3+6舍去).?
∴k=3-![]() ,?
,?
即当k=3-![]() 时,二面角AMCB的大小为
时,二面角AMCB的大小为![]() .
.

 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.