题目内容
(本题满分12分)
如图所示的几何体是由以正三角形 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.

(1)当 时,求平面
时,求平面 与平面
与平面 的夹角的余弦值;
的夹角的余弦值;
(2)当 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 ?
?
【答案】
(1)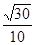 (2)2
(2)2
【解析】
试题分析:(1)分别取 、
、 的中点
的中点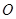 、
、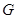 ,连接
,连接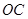 、
、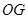 .
.
以直线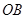 、
、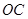 、
、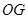 分别为
分别为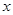 轴、
轴、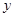 轴、
轴、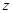 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
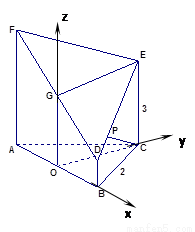
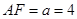 ,则
,则 、
、 、
、 的坐标分别为
的坐标分别为
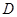 (1,0,1)、
(1,0,1)、 (0,
(0,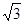 ,3)、
,3)、 (-1,0,4),
(-1,0,4),
∴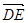 =(-1,
=(-1,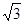 ,2),
,2),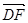 =(-2,0,3)
=(-2,0,3)
设平面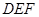 的法向量
的法向量 ,
,
由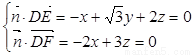 得
得
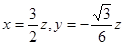 ,可取
,可取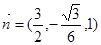 …… 3分
…… 3分
平面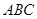 的法向量可以取
的法向量可以取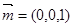
∴ …… 5分
…… 5分
∴平面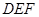 与平面
与平面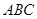 的夹角的余弦值为
的夹角的余弦值为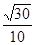 .
……6分
.
……6分
(2)在(1)的坐标系中,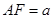 ,
,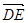 =(-1,
=(-1,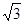 ,2),
,2),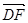 =(-2,0,
=(-2,0, -1).
-1).
因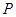 在
在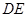 上,设
上,设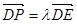 ,则
,则
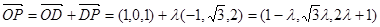
∴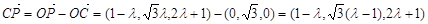
于是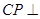 平面
平面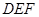 的充要条件为
的充要条件为
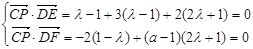
由此解得, ……10分
……10分
即当 =2时,在
=2时,在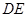 上存在靠近
上存在靠近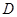 的第一个四等分点
的第一个四等分点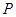 ,使
,使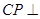 平面
平面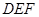 .
……12分
.
……12分
考点:空间向量求解二面角,判定线面垂直
点评:空间向量解决立体几何问题的关键是建立合适的坐标系,找准相关点的坐标

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面