题目内容
设斜率为k1的直线L交椭圆C:
+y2=1于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
+
=1(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
-
=1(a>0,b>0)中相类似的结论,并证明你的结论.
| x2 |
| 2 |
(1)求k1?k2的值.
(2)把上述椭圆C一般化为
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)设直线方程为y=k1x+b,代入椭圆方程并整理得:(1+2k12)x2+4k1bx+2b2-2=0,x1+x2=-
,又中点M在直线上,所以
=k1(
)+b,由此能求出k1?k2的值.
(2)对于椭圆,k1•k2=-
,已知斜率为k1的直线L交双曲线
-
=1(a>0,b>0)于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).则k1?k2的值为
.
解法一:设直线方程为y=k1x+d,代入
-
=1(a>0,b>0)方程并整理得:(b2-a2k12)x2-2k1a2dx-a2d2-a2b2=0,由此能求出k1•k2=
.
解法二:设点A(x1,y2),B(x2y2),中点M(x0,y0),则x0=
,y0=
K2=
=
K1=
,又因为点A,B在双曲线上,则
-
=1与
-
=1作差得到k1•k2=
.
| 4k1b |
| 1+2k1 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
(2)对于椭圆,k1•k2=-
| b2 |
| a2 |
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
解法一:设直线方程为y=k1x+d,代入
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
解法二:设点A(x1,y2),B(x2y2),中点M(x0,y0),则x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| y0 |
| x0 |
| y1+y2 |
| x1+x2 |
| (y2-y1) |
| (x2-x1) |
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
| b2 |
| a2 |
解答:(1)解:设直线方程为y=k1x+b,代入椭圆方程并整理得:
(1+2k12)x2+4k1bx+2b2-2=0,
x1+x2=-
,
又中点M在直线上,
∴
=k1(
)+b,
从而得弦中点M的坐标为(-
,
),
k2=-
,
∴k1k2=-
.
(2)对于椭圆,k1•k2=-
已知斜率为k1的直线L交双曲线
-
=1(a>0,b>0)于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).则k1?k2的值为
.
(解一)、设直线方程为y=k1x+d,
代入
-
=1(a>0,b>0)方程并整理,
得:(b2-a2k12)x2-2k1a2dx-a2d2-a2b2=0,
=k1(
)+d=
,
所以k2=
=
,
即k1•k2=
.
(解二)设点A(x1,y2),B(x2y2),中点M(x0,y0)
则x0=
,y0=
,
K2=
=
,
K1=
又因为点A,B在双曲线上,
则
-
=1与
-
=1,
作差得
=
=k1
,
即k1•k2=
.
(1+2k12)x2+4k1bx+2b2-2=0,
x1+x2=-
| 4k1b |
| 1+2k1 2 |
又中点M在直线上,
∴
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
从而得弦中点M的坐标为(-
| 2k1b |
| 1+2k2 |
| b |
| 1+2k2 |
k2=-
| 1 |
| 2k1 |
∴k1k2=-
| 1 |
| 2 |
(2)对于椭圆,k1•k2=-
| b2 |
| a2 |
已知斜率为k1的直线L交双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
(解一)、设直线方程为y=k1x+d,
代入
| x2 |
| a2 |
| y2 |
| b2 |
得:(b2-a2k12)x2-2k1a2dx-a2d2-a2b2=0,
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| b2d |
| b2-a2k12 |
所以k2=
| y1+y2 |
| x1+x2 |
| b2 |
| k1a2 |
即k1•k2=
| b2 |
| a2 |
(解二)设点A(x1,y2),B(x2y2),中点M(x0,y0)
则x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
K2=
| y0 |
| x0 |
| y1+y2 |
| x1+x2 |
K1=
| (y2-y1) |
| (x2-x1) |
又因为点A,B在双曲线上,
则
| x12 |
| a2 |
| y12 |
| b2 |
| x22 |
| a2 |
| y22 |
| b2 |
作差得
| a2 |
| b2 |
| (y2-y1)(y2+y1) | ||
(x2-x1)(
|
| k | 2 |
即k1•k2=
| b2 |
| a2 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,是高考的重点,易错点是计算繁琐,容易出错.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在). (a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线
(a>b>0),其它条件不变,试猜想k1与k2关系(不需要证明).请你给出在双曲线 (a>0,b>0)中相类似的结论,并证明你的结论.
(a>0,b>0)中相类似的结论,并证明你的结论.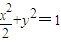 于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
于A、B两点,点M为弦AB的中点,直线OM的斜率为k2(其中O为坐标原点,假设k1、k2都存在).
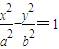 (a>0,b>0)中相类似的结论,并证明你的结论.
(a>0,b>0)中相类似的结论,并证明你的结论.