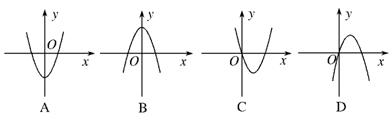
题目内容
下列图象中,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R且a≠0)的导函数f′(x)的图象,则f(-1)的值为

| 1 |
| 3 |
-
| 1 |
| 3 |
-
.| 1 |
| 3 |

分析:利用积的导数的运算法则求函数的导数,利用二次函数的图象和性质进行判断即可.
解答:解:因为f(x)=
x3+ax2+(a2-1)x+1(a∈R且a≠0),
所以f'(x)=x2+2ax+(a2-1)=(x+a-1)(x+a+1),则对应二次函数的图象开口向上,对应方程的两个根为1-a和-1-a.
所以不是第二个图象.
因为a≠0,所以f'(x)=x2+2ax+(a2-1)不是偶函数,所以图象不关于y轴对称,
所以不是第一个图象,所以第三个是导函数f′(x)的图象.
由图象可知,导函数f′(x)的图象过原点,所以f'(0)=a2-1=0,
解得a=1或a=-1,
当a=1时,对应方程的两个根分别为0,-2,不满足方程第二个根为正,所以不成立舍去.
当a=-1时,对应方程的两个根分别为0,2,满足方程第二个根为正,所以成立.
此时f(x)=
x3-x2+1,所以f(-1)=-
-1+1=-
.
故答案为:-
.
| 1 |
| 3 |
所以f'(x)=x2+2ax+(a2-1)=(x+a-1)(x+a+1),则对应二次函数的图象开口向上,对应方程的两个根为1-a和-1-a.
所以不是第二个图象.
因为a≠0,所以f'(x)=x2+2ax+(a2-1)不是偶函数,所以图象不关于y轴对称,
所以不是第一个图象,所以第三个是导函数f′(x)的图象.
由图象可知,导函数f′(x)的图象过原点,所以f'(0)=a2-1=0,
解得a=1或a=-1,
当a=1时,对应方程的两个根分别为0,-2,不满足方程第二个根为正,所以不成立舍去.
当a=-1时,对应方程的两个根分别为0,2,满足方程第二个根为正,所以成立.
此时f(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题主要考查导数的基本运算,二次函数的图象和性质,综合性较强.考查学生分析问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 下列图象中,有一个是函数f(x)=
下列图象中,有一个是函数f(x)= x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )
x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )


 或
或
 下列图象中,有一个是函数f(x)=
下列图象中,有一个是函数f(x)= x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )
x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )


 或
或
 x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函