题目内容
下列图象中,有一个是函数f(x)=| 1 | 3 |

分析:求出导函数,据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,故函数不是偶函数,得到函数的图象.
解答:解:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
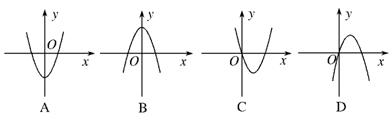
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
故答案为f(-1)=-
-1+1=-
.
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
故答案为f(-1)=-
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、
对称轴公式.
对称轴公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 下列图象中,有一个是函数f(x)=
下列图象中,有一个是函数f(x)= x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )
x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )


 或
或
 下列图象中,有一个是函数f(x)=
下列图象中,有一个是函数f(x)= x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )
x3+ax2+( a2-1)x+1(a∈R,a≠0)的导数f'(x)的图象,则f(-1)的值为( )


 或
或
 x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函