题目内容
函数f(x)= 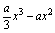 +x+1在x=x1,及x=x2处有极值,且1<
+x+1在x=x1,及x=x2处有极值,且1<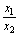 ≤5.
≤5.
(1)求a的取值范围;
(2)当a取最大值时,存在t∈R,使x∈[1,m](m>1)时,f’(t-x) ≤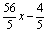 恒成立,试求m的最大值。
恒成立,试求m的最大值。
(1) 答案:由题设知f’(x)=ax2-2ax+1二根为x1、x2,
且x1+x2=2,x1x2=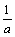 ,∵1<
,∵1<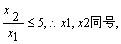
又x1+x2=2>0, ∴x1,x2同为正数,由1< 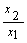 ≤5得x1<x2≤5x1,又∵x2=2-x1, ∴x1<2-x1≤5x1
≤5得x1<x2≤5x1,又∵x2=2-x1, ∴x1<2-x1≤5x1
整理得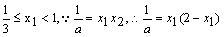
=-(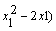 =-(x1-1)2+1.由x1∈[
=-(x1-1)2+1.由x1∈[ ,1]
,1]
得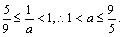


练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 nx B.-sinx C.cosx D.-cosx
nx B.-sinx C.cosx D.-cosx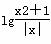 (x≠0,x∈R),有下列命题:
(x≠0,x∈R),有下列命题: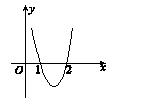
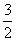 时,函数f(x)取得极小值;②f(x)有两个极值点;③当x=2时,函数f(x)取得极小值;④当x=1时,函数f(x)取得极大值.
时,函数f(x)取得极小值;②f(x)有两个极值点;③当x=2时,函数f(x)取得极小值;④当x=1时,函数f(x)取得极大值. ,则tan2α= .
,则tan2α= . 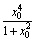 ;
;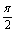 <an+1-an<π.
<an+1-an<π. 1)}(n∈N*) 为等差数列,且a1=3,a2=5,则
1)}(n∈N*) 为等差数列,且a1=3,a2=5,则
 = ( )
= ( ) C.1 D.
C.1 D.
