题目内容
如图，三棱锥
中，
底面
，
，
，
为
的中点，点
在
上，且
．
（1）求证：平面
平面
；
（2）求平面
与平面
所成的二面角的平面角（锐角）的余弦值．
 |
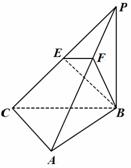（1）证明：∵
底面，且
底面， ∴
………1分
由，可得
…………………………2分
又
，∴
平面
………………3分
注意到
平面， ∴
…………………4分
,为中点，∴
………………………5分
， 
平面
……………………6分
而平面，∴
……………7分
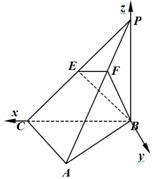
（2）方法一、如图，以
为原点、
所在直线为
轴、
为
轴建立空间直角坐标系．
则
…………………………8分
． ………………………10分
设平面的法向量
．
由
得
，
即
……………（1）
……………（2）
取
，则
，
． ……………12分
取平面的法向量为
 |
则
，
故平面与平面
所成角的二面角（锐角）的余弦值为
． ……………14分
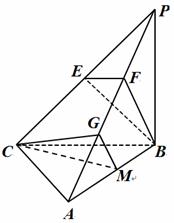
方法二、取
的中点
，
的中点
，连接
，
，
，∴
． ……………8分
， ∴
． ……………9分
同理可证：
． 又
， ∴
．……10分
则
与平面所成的二面角的平面角（锐角）就等于平面与平面所成的二面角的平面角（锐角）
已知
，
，
平面
∴
，∴
…………11分
 |
又
，∴
平面
由于
平面， ∴
而
为与平面的交线，
又
底面，平面
为二面角
的平面角
…………12分
根据条件可得
，
在
中，
在
中，由余弦定理求得
…………13分
故平面与平面所成角的二面角（锐角）的余弦值为． …………14分
第1卷单元月考期中期末系列答案
如图，三棱锥
中，
底面
，
，
，点
、
分别是
、
的中点.
；（2）求二面角
的余弦值。
中，
底面
，
，
，点
、
分别是
、
的中点.
；（Ⅱ）求二面角
的大小.
中，
^底面
，若底面
与底面
．若
是
的中点，求：
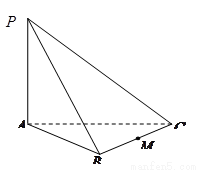
与
所成角的大小（结果用反三角函数值表示）．
中，
底面
，
，
，
为
的中点，点
在
上，且
.
平面
； 
与平面
所成的二面角的平面角（锐角）的余弦值.
中，
^底面
，若底面
，若
是
的中点，
与
所成角的大小（结果用反三角函数值表示）.