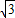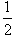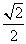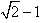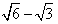题目内容
已知椭圆对称轴为坐标轴,离心率 且经过点
且经过点 ,求椭圆方程.
,求椭圆方程.
解:由e= =
= 可得b=
可得b= a,因此设椭圆方程为(1)
a,因此设椭圆方程为(1)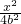 +
+ =1或(2)
=1或(2)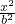 +
+ =1,
=1,
将点(4,2 )的坐标代入可得(1)b2=16,(2)b2=19,
)的坐标代入可得(1)b2=16,(2)b2=19,
∴所求方程是:
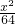 +
+ =1或
=1或 +
+ =1.
=1.
分析:由椭圆的离心率e= =
= 可得b=
可得b= a,从而可设出椭圆的两种形式的标准方程,再将点(4,2
a,从而可设出椭圆的两种形式的标准方程,再将点(4,2 )的坐标代入可得求得答案.
)的坐标代入可得求得答案.
点评:本题考查椭圆的标准方程,考查待定系数法,准确设出椭圆的两种标准方程是关键,属于中档题.
 =
= 可得b=
可得b= a,因此设椭圆方程为(1)
a,因此设椭圆方程为(1)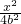 +
+ =1或(2)
=1或(2)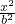 +
+ =1,
=1,将点(4,2
 )的坐标代入可得(1)b2=16,(2)b2=19,
)的坐标代入可得(1)b2=16,(2)b2=19,∴所求方程是:
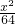 +
+ =1或
=1或 +
+ =1.
=1.分析:由椭圆的离心率e=
 =
= 可得b=
可得b= a,从而可设出椭圆的两种形式的标准方程,再将点(4,2
a,从而可设出椭圆的两种形式的标准方程,再将点(4,2 )的坐标代入可得求得答案.
)的坐标代入可得求得答案.点评:本题考查椭圆的标准方程,考查待定系数法,准确设出椭圆的两种标准方程是关键,属于中档题.

练习册系列答案
相关题目

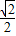
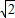 -1
-1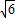 -
-