题目内容
不等式|2x+1|-|x-4|＞2的解集为 ．
【答案】分析：通过对x分类讨论①当x＞4时，②当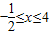
时，③当
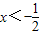时，去掉绝对值符号即可得出．
解答：解：①当x＞4时，|2x+1|-|x-4|=2x+1-（x-4）=x+5，∴x+5＞2，解得x＞-3，又x＞4，∴x＞4；
②当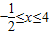
时，原不等式可化为2x+1+x-4＞2，解得
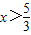，又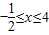
，∴
；
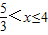③当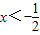
时，原不等式可化为-2x-1+x-4＞2，解得x＜-7，又
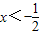，∴x＜-7．
综上可知：原不等式的解集为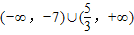
．
故答案为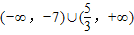
．
点评：熟练掌握分类讨论思想方法是解含绝对值的不等式的常用方法之一．
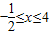时，③当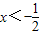时，去掉绝对值符号即可得出．解答：解：①当x＞4时，|2x+1|-|x-4|=2x+1-（x-4）=x+5，∴x+5＞2，解得x＞-3，又x＞4，∴x＞4；
②当
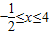时，原不等式可化为2x+1+x-4＞2，解得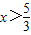，又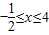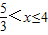，∴；③当
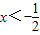时，原不等式可化为-2x-1+x-4＞2，解得x＜-7，又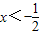，∴x＜-7．综上可知：原不等式的解集为
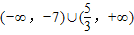．故答案为
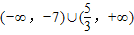．点评：熟练掌握分类讨论思想方法是解含绝对值的不等式的常用方法之一．
练习册系列答案
阅读快车系列答案
相关题目