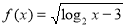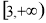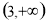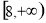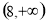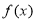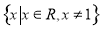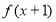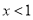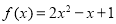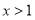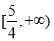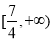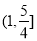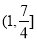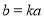题目内容
已知函数
(1)求函数 的定义域和值域;
的定义域和值域;
(2)若 有最小值-2,求
有最小值-2,求 的值.
的值.
(1) 的定义域是
的定义域是 .当
.当 时,
时, 值域为
值域为 ;(2)
;(2)
【解析】
试题分析:(1)由对数函数的定义可得 ,解此不等式组,从而求得函数的定义域;首先对函数解析式进行化归,考虑到对数函数中底数的范围制约着函数单调性,影响到函数的值域,所以需要对底数
,解此不等式组,从而求得函数的定义域;首先对函数解析式进行化归,考虑到对数函数中底数的范围制约着函数单调性,影响到函数的值域,所以需要对底数 的范围进行分类讨论,从求出函数的值域;(2)根据(1)中函数值的分布情况,可知只有当
的范围进行分类讨论,从求出函数的值域;(2)根据(1)中函数值的分布情况,可知只有当 时,函数
时,函数 有最小值,所以有
有最小值,所以有 ,从而解得所求
,从而解得所求 的值.
的值.
试题解析:(1)依题意 得
得
则 ,
,
 ,
, 3分
3分
当 时,
时, ;当
;当 时,
时,
 的定义域是
的定义域是 .当
.当 时,
时, 值域为
值域为
当 时,
时, 值域为
值域为 . 7分
. 7分
(2)因为 有最小值-2,由(1)可知
有最小值-2,由(1)可知 且
且 ,
,

 12分
12分
考点:1.函数的定义域;2.对数函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目