题目内容
设双曲线 的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
的左、右焦点分别为F1、F2,A是双曲线渐近线上的一点,AF2⊥F1F2,原点O到直线AF1的距离为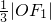 ,则渐近线的斜率为
,则渐近线的斜率为
- A.

- B.

- C.1或-1
- D.

D
分析:设出点A的坐标,确定直线AF1的方程,利用点到直线的距离公式,及原点O到直线AF1的距离为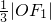 ,建立方程,即可求得渐近线的斜率.
,建立方程,即可求得渐近线的斜率.
解答:双曲线的渐近线方程为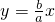
不妨设A在第一象限,则A(c, ),
),
∴直线AF1的方程为
即
∴原点O到直线AF1的距离为
∵原点O到直线AF1的距离为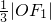 ,
,
∴
∴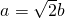
∴
故选D.
点评:本题考查双曲线的几何性质,考查点到直线的距离公式,考查学生的计算能力,属于中档题.
分析:设出点A的坐标,确定直线AF1的方程,利用点到直线的距离公式,及原点O到直线AF1的距离为
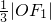 ,建立方程,即可求得渐近线的斜率.
,建立方程,即可求得渐近线的斜率.解答:双曲线的渐近线方程为
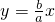
不妨设A在第一象限,则A(c,
 ),
),∴直线AF1的方程为

即

∴原点O到直线AF1的距离为

∵原点O到直线AF1的距离为
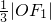 ,
,∴

∴
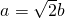
∴

故选D.
点评:本题考查双曲线的几何性质,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
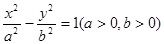 的左、右焦点分别为
的左、右焦点分别为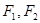 ,离心率为
,离心率为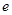 ,过
,过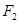 的直线与双曲线的右支交于
的直线与双曲线的右支交于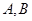 两点,若
两点,若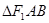 是以
是以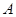 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则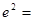 _______.
_______.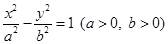 的左、右焦点分别为
的左、右焦点分别为 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,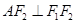 ,原点
,原点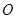 到直线
到直线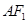 的距离为
的距离为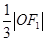 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)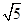 或
或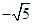 (B)
(B)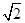 或
或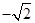 (C)1或
(C)1或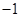 (D)
(D)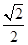 或
或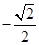
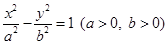 的左、右焦点分别为
的左、右焦点分别为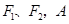 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,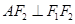 ,原点
,原点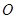 到直线
到直线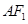 的距离为
的距离为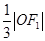 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)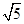 或
或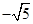 (B)
(B)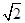 或
或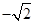 (C)1或
(C)1或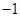 (D)
(D)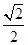 或
或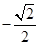
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,过点
,过点 、
、 .若△
.若△ 为正三角形,则该双曲线的离心率为
为正三角形,则该双曲线的离心率为
 B.
B. C.
C. D.
D.