Question

在正四面体ABCD中，点E、F分别为BC、AD的中点，则AE与CF所成角的余弦值为（　　）

• A、-

  2

  3

• B、

  2

  3

• C、-

  1

  3

• D、

  1

  3

Answer 1

分析：通过建立空间直角坐标系，利用向量的夹角即可得出异面直线的夹角．

解答：解：如图所示，作AO⊥底面BCD，垂足为O，O为底面等边△BCD的中心，建立空间直角坐标系．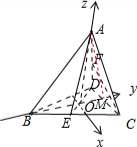
不妨取CD=2．则C（1，

3

3

，0），D(-1，

3

3

，0)，B(0，-

2 3

3

，0)，
E(

1

2

，-

3

6

，0)，
设点M是线段CD的中点，则AM=

3

，OM=

1

3

BM=

3

3

．
∴AO=

(AM)2-(OM)2

=

( 3 )2-( 3 3 )2

=

2 6

3

．
∴A(0，0，

2 6

3

)．
∴F(-

1

2

，

3

6

，

6

3

)，
∴

AE

=(

1

2

，-

3

6

，-

2 6

3

)，

CF

=(-

3

2

，-

3

6

，

6

3

)．
∴cos＜

AE

，

CF

＞=

AE • CF

| AE | | CF |

=

- 3 4 + 1 12 - 4 3

3 × 3

=-

2

3

．
∴异面直线AE与CF所成角的余弦值为

2

3

．
故选：B．

点评：本题考查了通过建立空间直角坐标系利用向量的夹角求异面直线的夹角的方法，属于中档题．