题目内容
(本大题满分12分)定义在![]() 上的函数
上的函数![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,且对任意的
,且对任意的![]() 、
、![]() ,有
,有![]() ,
,
求证:(1)![]() ;(2)对任意的
;(2)对任意的![]() ,恒有
,恒有![]() ;
;
(3)证明:![]() 是
是![]() 上的增函数;(4)若
上的增函数;(4)若![]() ,求
,求![]() 的取值范围。
的取值范围。
(1)令a=b=0,则f(0)=[f(0)]2∵f(0)≠0 ∴f(0)=1 …………………2分
(2)令a=x,b=-x则 f(0)=f(x)f(-x) ∴![]()
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴![]() 又x=0时,f(0)=1>0∴对任意x∈R,f(x)>0 …………6分
又x=0时,f(0)=1>0∴对任意x∈R,f(x)>0 …………6分
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴![]() ∴f(x2)>f(x1) ∴f(x)在R上是增函数…9分
∴f(x2)>f(x1) ∴f(x)在R上是增函数…9分
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)又1=f(0),
f(x)在R上递增∴由f(3x-x2)>f(0)得:3x-x2>0 ∴ 0<x<3 ………………12分

练习册系列答案
相关题目
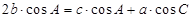 ,
,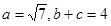 ,求△ABC的面积.
,求△ABC的面积. 中,
中, 分别为内角
分别为内角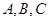 的对边,且
的对边,且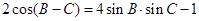
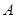
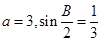 ,求
,求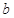
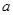 为实常数,函数
为实常数,函数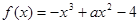 ,
,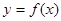 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为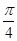 ,求函数
,求函数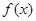 的单调区间;
的单调区间;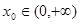 ,使
,使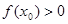 ,求
,求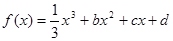 的图象过点(0,3),且在
的图象过点(0,3),且在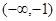 和
和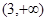 上为增
上为增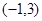 上为减函数.
上为减函数.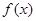 的解析式;
的解析式;