题目内容
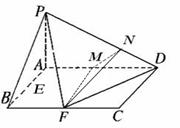
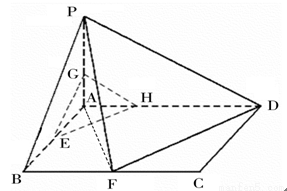
(本小题满分l2分)已知在四棱锥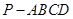 中,底面
中,底面 是矩形,且
是矩形,且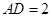 ,
, ,
,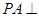 平面
平面 ,
, 、
、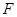 分别是线段
分别是线段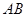 、
、 的中点.
的中点.
(1)证明: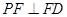 ;
;
(2)判断并说明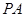 上是否存在点
上是否存在点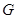 ,使得
,使得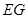 ∥平面
∥平面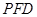 ;
;
(3)若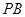 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角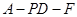 的余弦值.
的余弦值.

(1)见解析
(2)满足AG=1/4AP的点G即为所求
(3)
【解析】解:解法一:(Ⅰ)∵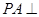 平面ABCD,
平面ABCD,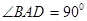 ,
,
AB=1,AD=2,建立如图所示的空间直角坐标系A-xyz,
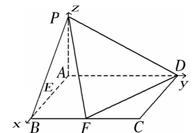
则A(0,0,0)B(1,0,0)F(1,1,0)D(0,2,0).,………2分
不妨令P(0,0,t)∵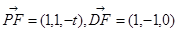 ,
,
∴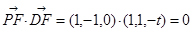 ,
,
即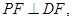 .…………………………4分
.…………………………4分
(Ⅱ)设平面PFD的法向量为,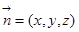
由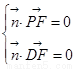 ,得
,得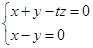 ,令z=1,解得:x=y=t/2.
,令z=1,解得:x=y=t/2.
∴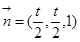 . ………………………………………………………6分
. ………………………………………………………6分
设G点坐标为(0,0,m),E(1/2,0,0),则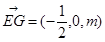 ,
,
要使EG∥平面PFD,只需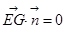 ,即,
,即,
得m=1/4t,从而满足AG=1/4AP的点G即为所求.……………………………8分
(Ⅲ)∵ ,∴
,∴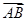 是平面
是平面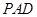 的法向量,易得
的法向量,易得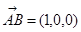 ,
,
…………………………………………………………………………………9分
又∵PA平面ABCD,∴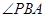 是PB与平面ABCD所成的角,
是PB与平面ABCD所成的角,
得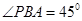 ,PA=1,平面PFD的法向量为
,PA=1,平面PFD的法向量为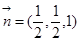 ……10分
……10分
∴ ,
,
故所求二面角A=PD-F的余弦值为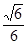 .………12分
.………12分
解法二:(Ⅰ)证明:连接AF,则AF=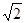 ,DF=
,DF=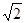 ,
,
又AD=2,∴ 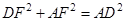 ,∴
,∴ 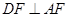 ……2分
……2分
又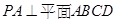 ,∴
,∴ 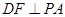 ,又
,又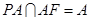 ,
,
∴ 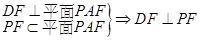 ……4分
……4分
(Ⅱ)过点E作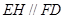 交
交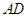 于点
于点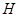 ,则
,则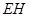 ∥平面
∥平面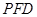 ,且有
,且有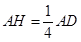 …5分
…5分
再过点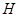 作
作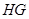 ∥
∥ 交
交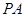 于点
于点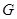 ,则
,则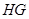 ∥平面
∥平面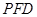 且
且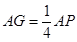 ,
,
∴ 平面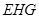 ∥平面
∥平面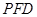 …………………7分∴
…………………7分∴ 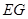 ∥平面
∥平面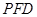 .
.
从而满足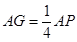 的点
的点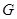 即为所求. ……………………………………………8分
即为所求. ……………………………………………8分
(Ⅲ)∵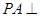 平面ABCD,∴
平面ABCD,∴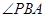 是PB与平面ABCD所成的角,且
是PB与平面ABCD所成的角,且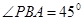 .
.
∴ PA=AB=1 ………………………………………………………………9分
取AD的中点M,则FM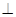 AD,FM
AD,FM 平面PAD,
平面PAD,
在平面PAD中,过M作MN PD于M,连接FN,则PD
PD于M,连接FN,则PD 面FMN,
面FMN,
则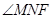 即为二面角A-PD-F的平面角………………………10分
即为二面角A-PD-F的平面角………………………10分
∵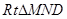 ∽
∽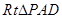 ,∴
,∴ 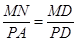 ,
,
∵ ,且
,且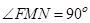
∴ 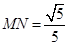 ,
,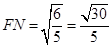 ,
,
∴  ……………12分
……………12分

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线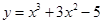 相切的直线方程.
相切的直线方程.