题目内容
已知a，b，c为△ABC的三个内角A，B，C的对边，向量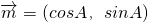
，
，若
⊥
，且acosB+bcosA=csinC，则角B=
- A.
- B.
- C.
- D.
A
分析：先根据⊥推断两向量的积为0求得tanA的值，进而其求得A，进而利用正弦定理分别表示出a和c代入题设等式中化简整理求得sinC的值，进而求得C，最后利用三角形内角和求得答案．
解答：∵⊥，
∴•=
cosA-sinA=0
∴tanA=，A=60°
三角形正弦定理：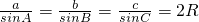
∴a=
c=b
∵acosB+bcosA=csinC，
∴acosB+bcosA=csinC=
∴cosB+bcosA=
整理得sinAcosB+cosAsinB=（sinC）2
∵A+B+C=180∴A+B=180-C
∴sin（A+B）=sinC=（sinC）2
∴sinC=1
∴C=90°∴B=90°-60°=30°
故选A
点评：本题主要考查了正弦定理应用．考查了学生综合分析问题和基本的运算能力．
分析：先根据
⊥推断两向量的积为0求得tanA的值，进而其求得A，进而利用正弦定理分别表示出a和c代入题设等式中化简整理求得sinC的值，进而求得C，最后利用三角形内角和求得答案．解答：∵
⊥，∴
•=cosA-sinA=0∴tanA=
，A=60°三角形正弦定理：
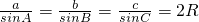
∴a=
c=b ∵acosB+bcosA=csinC，
∴acosB+bcosA=csinC=
∴
cosB+bcosA= 整理得sinAcosB+cosAsinB=（sinC）2
∵A+B+C=180∴A+B=180-C
∴sin（A+B）=sinC=（sinC）2
∴sinC=1
∴C=90°∴B=90°-60°=30°
故选A
点评：本题主要考查了正弦定理应用．考查了学生综合分析问题和基本的运算能力．
练习册系列答案
相关题目