题目内容
6. 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.(Ⅰ)求证:MN∥平面PAB;
(Ⅱ)若平面ABCD⊥平面PAD,求直线MN与平面ABCD所成角的正切值.
分析 (1)取PC中点Q,可证面NQM∥面PAB,得MN∥面PAB;
(2)过N作NO⊥AD,连接MO,则直线MN与平面ABCD所成的角为∠MNO,即可求解.
解答 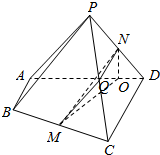 (I)证明:取PC中点Q,连接MQ,NQ.…(2分)
(I)证明:取PC中点Q,连接MQ,NQ.…(2分)
∵M,Q分别是BC,PC的中点,
∴MQ∥BP,∴MQ∥平面PAB.…(4分)
同理可证:NQ∥CD∥AB,∴NQ∥平面PAB…(5分)
∴面NQM∥面PAB,得MN∥面PAB; …(7分)
(Ⅱ)解:过N作NO⊥AD,
∵平面ABCD⊥平面PAD,
∴NO⊥平面ABCD,
连接MO,则直线MN与平面ABCD所成的角为∠MNO…(10分)
在△MNO中,$NO=\frac{3}{4},OM=\frac{{\sqrt{39}}}{4}$…(13分)
直线MN与平面ABCD所成角的正切值为$tan∠NMO=\frac{NO}{MO}=\frac{{\sqrt{39}}}{13}$. …(15分)
点评 本题考查的知识点是直线与平面所成角及求法,直线与平面平行的判定,平面与平面平行的判定与性质,难度中档.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
16.阅读如图所示的程序框图,运行相应的程序,则输出的结果s=( )


| A. | 0 | B. | 1 | C. | 3 | D. | 4 |
17.执行如图所示的程序框图(算法流程图),输出的n为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.等差数列{an}的前n项和为Sn,且4a1,2a2,a3成等比数列.若a1=3,则S4=( )
| A. | 7 | B. | 8 | C. | 12 | D. | 16 |
11.已知函数f(x)的定义域是[-1,2],则y=f(x)+f(-x)的定义域是( )
| A. | [-1,1] | B. | [-2,2] | C. | [-1,2] | D. | [-2,1] |
18.等比数列{an}的前n 项和为S n,若an>0,q>1,a3+a5=20,a2a6=64则公比q为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
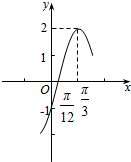 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).