题目内容
8.已知数列{an}满足:a1=1,an+1=$\frac{a_n}{{2{a_n}+3}}$(n∈N*),则a4=$\frac{1}{53}$.分析 由已知得$\frac{1}{{a}_{n+1}}=\frac{2{a}_{n}+3}{{a}_{n}}$=$\frac{3}{{a}_{n}}$+2,从而得到{$\frac{1}{{a}_{n}}+1$}是首项为2,公比为3的等比数列,由此能求出a4.
解答 解:∵数列{an}满足:a1=1,an+1=$\frac{a_n}{{2{a_n}+3}}$(n∈N*),
∴$\frac{1}{{a}_{n+1}}=\frac{2{a}_{n}+3}{{a}_{n}}$=$\frac{3}{{a}_{n}}$+2,
∴$\frac{1}{{a}_{n+1}}+1=3(\frac{1}{{a}_{n}}+1)$,
又$\frac{1}{{a}_{1}}+1$=2,
∴{$\frac{1}{{a}_{n}}+1$}是首项为2,公比为3的等比数列,
∴$\frac{1}{{a}_{n}}+1=2×{3}^{n-1}$,
∴${a}_{n}=\frac{1}{2×{3}^{n-1}-1}$,
∴${a}_{4}=\frac{1}{2×{3}^{3}-1}$=$\frac{1}{53}$.
故答案为:$\frac{1}{53}$.
点评 本题考查数列的第4项的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.cos(-$\frac{67}{6}$π)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18. 函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )
函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )
 函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )
函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )| A. | 2011 | B. | $\frac{4023}{2}$ | C. | 2012 | D. | $\frac{4025}{2}$ |
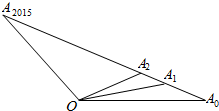 如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).
如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).