题目内容
设函数f（x）=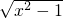
+
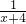的定义域为A，函数y=log2 （ x2-5x-6 ） 的定义域为B 求：
（1）A，B；
（2）A∩B，A∪B，CRB．
解：（1）函数f（x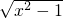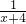）=+有意义
则
解得x≤-1或x≥1且x≠-4
∴A={x|x≤-1或x≥1且x≠-4}
函数y=log2 （ x2-5x-6 ）有意义
则 x2-5x-6＞0解得x＞6或x＜-1
∴B={x|x＞6或x＜-1}
（2）A∩B={x|x＞6或x＜-1且x≠-4}
A∪B={x|x≤-1或x≥1}
CRB={x|-1≤x≤6}
分析：（1）根据根式及分式有意义的条件，以及偶次根式有意义可得集合A，根据对数函数的真数大于零可求出集合B；
（2）根据交集的定义，并集的定义，以及补集的定义可求出所求．
点评：本题属于以函数的定义域的求解为平台，进而求集合的交集、补集、并集的运算的基础题，也是高考常会考的基础的题型．
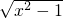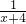+有意义则
解得x≤-1或x≥1且x≠-4∴A={x|x≤-1或x≥1且x≠-4}
函数y=log2 （ x2-5x-6 ）有意义
则 x2-5x-6＞0解得x＞6或x＜-1
∴B={x|x＞6或x＜-1}
（2）A∩B={x|x＞6或x＜-1且x≠-4}
A∪B={x|x≤-1或x≥1}
CRB={x|-1≤x≤6}
分析：（1）根据根式及分式有意义的条件，以及偶次根式有意义可得集合A，根据对数函数的真数大于零可求出集合B；
（2）根据交集的定义，并集的定义，以及补集的定义可求出所求．
点评：本题属于以函数的定义域的求解为平台，进而求集合的交集、补集、并集的运算的基础题，也是高考常会考的基础的题型．
练习册系列答案
相关题目
设函数f（x）=log2x的反函数为y=g（x），若g(
)=
，则a等于（ ）
| 1 |
| a-1 |
| 1 |
| 4 |
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
设函数f（x）=2x的反函数为y=f-1（x），则f-1（1）=（ ）
| A、0 | ||
| B、1 | ||
C、
| ||
| D、2 |