题目内容
对数列![]() ,规定
,规定![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() 。对正整数k,规定
。对正整数k,规定![]() 为
为![]() 的k阶差分数列,其中
的k阶差分数列,其中![]() 。
。
(1) 若数列![]() 首项
首项![]() ,且满足
,且满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2) 对(1)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切正整数
对一切正整数![]() 都成立?若存在,求数列
都成立?若存在,求数列![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3) 令![]() ,设
,设![]() ,若
,若![]() 恒成立,求最小的正整数M的值。
恒成立,求最小的正整数M的值。
解析:(1)![]() 而
而![]() 可得
可得![]()
![]() ,
,![]() ,…………………… 2分
,…………………… 2分
![]()
![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
![]() ,
,![]() (
(![]() ) …………………… 4分
) …………………… 4分
(2)![]() 即:
即:![]()
而又![]()
所以![]() …………………… 6分
…………………… 6分
=![]() 故可得
故可得![]()
![]() 存在等差数列
存在等差数列![]() ,
,![]() 使
使
![]() 对一切正整数
对一切正整数![]() 都成立。…………………… 8分
都成立。…………………… 8分
(3)由(2)知 ![]() ……… ①
……… ①
![]() ……… ② …………………… 10分
……… ② …………………… 10分
①-②得:![]()
![]() …………………… 12分
…………………… 12分
![]() ,
,![]() 递增 ,且
递增 ,且![]() 。
。
![]() 满足条件的最小的正整数M的值为6. …………………… 14分
满足条件的最小的正整数M的值为6. …………………… 14分

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 ,规定
,规定 为数列
为数列 N*).对正整数k,规定
N*).对正整数k,规定 为
为 .
. ,且满足
,且满足 ,求数列
,求数列 是等差数列,使得
是等差数列,使得 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
; 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值. ,规定
,规定 为数列
为数列 .对自然数
.对自然数 ,规定
,规定 为数列
为数列

 ,则
,则 ;
; ,且满足
,且满足 ,则数列
,则数列 ,规定
,规定 为数列
为数列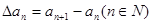 , 对自然数
, 对自然数 ,规定
,规定 为
为 .
. ,试判断
,试判断 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?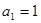 ,且满足
,且满足 ,求数列
,求数列 ,使得
,使得 对一切自然
对一切自然 都成立?若存在,求数列
都成立?若存在,求数列 ,规定
,规定 为数列
为数列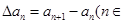 N*).对正整数k,规定
N*).对正整数k,规定  为
为 .
. ,且满足
,且满足 ,求数列
,求数列 是等差数列,使得
是等差数列,使得 对一切正整数
对一切正整数 N*都成立,求
N*都成立,求 ;
; 设
设 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值.